Hyperbola - 5
CONJUGATE HYPERBOLA
The hyperbola whose transverse & conjugate axes are respectively the conjugate & transverse axes of the standard hyperbolais called the conjugate hyperbola of the standard given hyperbola. The conjugate hyperbola of 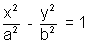 is
is 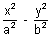 = - 1.
= - 1.
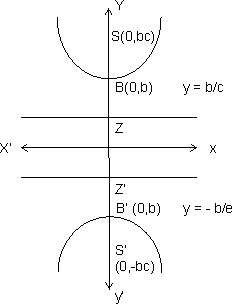
SOME RESULTS OF CONJUGATE HYPERBOLA
(a) Length of Transverse axis = 2b
(b) Length of conjugate axis = 2a
© Foci = (0, ±be)
(d) Equation of Directrices = y = ± b/e
(e) Eccentricity = e =
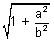
(f) Length of Latus Rectum =
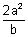
(g) Parametric co-ordinates = (a tan
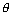 , b sec
, b sec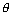 )
) (h) Equation of transverse axis = x = 0
(i) Equation of conjugate axis = y = 0
Illustration : 11.
Find the length of transverse axis, conjugate axis eccentricity, coordinates of foci, vertices, length of latus rectum & equation of directrices of the hyperbola 9x2 - 4y2 = - 36.
Ans: The hyperbola is
9x2 - 4y2 = - 36
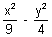 = - 1 i.e of the form
= - 1 i.e of the form 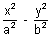 = - 1 where a = 2 & b = 3
= - 1 where a = 2 & b = 3 Length of transverse axis = 2b = 6units
Length of conjugation axis = 2a = 4 units
Eccentricity =

Vertices = (0, ± b) = (0, ± 3)
Length of Latus Rectum =
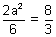 units
units Equation of directrices = y = ± b/e
= y = ±
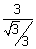
= y = ±
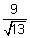
= y = ±

RECTANGULAR HYPERBOLA DEFINITION
(1) A hyperbola whose asymptotes include aright angle is called a rectangular Hyperbola. THe general form of the equation of hyperbola is x2 - y2 = a2 = b2.
Why ?
The asysmptotes of a hyperbola is
y = ±
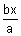
If these are at right angles than
m1m2 = - 1
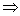
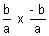 = - 1
= - 1 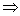 b2 = a2
b2 = a2Hence the equation of ractangular hyperbola is
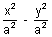 = 1
= 1 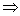 x2 - y2 = a2
x2 - y2 = a2 (2) If the length of transverse & conjugate axes of any hyperbola are equal, it is called as rectangular hyperbola.
Why ?
IF a = b, then
 = 1 become
= 1 become 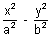 = 1
= 1 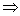 x2 - y2 = a2
x2 - y2 = a2RECTANGULAR HYPERBOLA (xy = c2)
The equation of Rectangular Hyperbola is x2 - y2 = a2
i.e. (x + y)(x - y) = a2
We know that x + y =0 & x - y = 0 are at 450 & 1350 to the x axis. Now if we can rotate the axes through
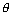 = - 450 without changing the origin.
= - 450 without changing the origin. So, we can replace (x, y) by
(x cos
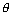 - y sin
- y sin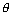 , x sin
, x sin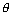 + y cos
+ y cos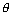 ) i.e.
) i.e. 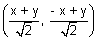
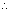 The equation x2 - y2 = a2 becomes
The equation x2 - y2 = a2 becomes 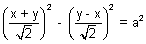
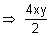 = a2
= a2 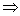 xy =
xy = 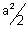
Let
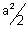 = c2 = any positive constant
= c2 = any positive constant Therefore xy = c2 is the another form of Rectangular hyperbola.
RESULTS OF RECTANGULAR HYPERBOLA
(a) The parametric coordinates are x = ct & y = c/t.
(b) Equation of chord joining t1 & t2 is
x + yt1t2 = c(t1 + t2)
© Equation of tangent at t is
 + yt = x.
+ yt = x.(d) Point of intersection of tangents at ’t1’ & ’t2’ is
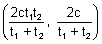 .
. (e) Equation of normal at ’t’ is
xt3 - yt - ct4 + c = 0.
(f) Points of intersection of normals at ’t1’ & ’t2’ is
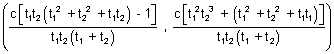
Illustration : 12.
Find the eccentricity of Rectangular Hyperbola.
Ans: For the hyperbola
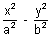 = 1; c =
= 1; c = 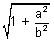
Therefore for
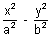 = 1 we have b = a
= 1 we have b = a Hence eccentricity of Rectangular hyperbola is
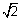 .
. Easy
1. For what value of k does
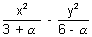 = 1 represents a hyperbola ?
= 1 represents a hyperbola ? Ans: We know that the standard form of hyperbola can be
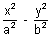 = 1 or
= 1 or 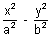 = - 1.
= - 1. CASE - I
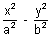 = 1
= 1 As a2 & b2 are +ve quantities greater than zero simultaneously, therefore
3 +
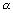 > 0 & 6 -
> 0 & 6 - 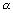 > 0
> 0 
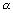 > - 3 &
> - 3 & 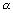 < 6
< 6 Hence common solution is
- 3 <
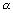 < 6
< 6 CASE II
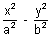 = - 1 or
= - 1 or  = 1
= 1 Here also - a2 & - b2 are -ve quantities.
Therefore
3 +
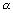 < 0 & also 6 -
< 0 & also 6 - 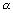 < 0
< 0 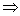
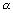 < - 3 &
< - 3 & 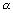 > 6
> 6 There is no common solution.
Hence the only solution is
- 3 <
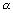 < 6 or
< 6 or 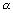
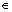 (- 3, 6)
(- 3, 6) Q.2. Find the value of c if the ellipse
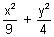 = 1 & x2 - y2 = c2 cut at right angles ?
= 1 & x2 - y2 = c2 cut at right angles ? Ans: The curves cut at right angle means that the tangents at the point of intersection of two curves are at right angles. If m1 is the slope of the tangent to ellipse & m2 is the slope of the tangent to hyperbola, then
m1 =
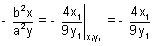 …………………….. (i)
…………………….. (i) m2 =
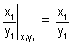 ………………………………… (ii)
………………………………… (ii)using (i) & (ii)
m1m2 = - 1
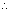
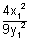 = 1
= 1 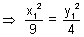
But
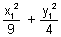 = 1 as (x1y1) lies on hyperbola
= 1 as (x1y1) lies on hyperbola 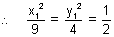
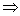 x12 = 9⁄2 ………………………………………… (iii)
x12 = 9⁄2 ………………………………………… (iii) y12 = 4⁄2 ……………………………………….. (iv)
Bur x12 - y12 = c2 …………………………………… (v)
Using (iii) & (iv) in (v) we get
c2 =
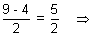 c = ±
c = ± 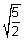
Q.3. Prove that if normal to the hyperbola xy = c2 at any point t1 meets the curve again at t2, then, t13t2 = - 1.
Ans: Equation of normal at point t1 is
yt1 - xt13 = c - ct14
Now if this normal again meets at ’t2’, then (ct2,
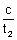 ) must satisfy the normal
) must satisfy the normal 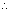
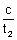 t1 - ct2t13 = c - ct14
t1 - ct2t13 = c - ct14 ct13[t2 - t1] =
ct13[t2 - t1] = 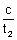 [t1 - t2]
[t1 - t2] 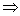 ct13t2[t2 - t1] + c(t2 - t1) = 0
ct13t2[t2 - t1] + c(t2 - t1) = 0 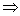 c(t2 - t1)(t13 + 1) = 0
c(t2 - t1)(t13 + 1) = 0 As t2
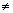 t1 & c > 0
t1 & c > 0 t13t2 + 1 = 0
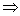 t13t2 = - 1
t13t2 = - 1 Q.4. If (a sec
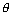 , b tan
, b tan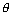 ) & (a sec
) & (a sec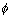 , b tan
, b tan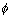 ) are the end points of a focal chord of the hyperbola
) are the end points of a focal chord of the hyperbola 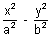 = 1, then prove that tan
= 1, then prove that tan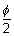 tan
tan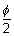 =
= 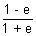 .
. Ans: The equation of chord joining the points (a sec
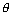 , b tan
, b tan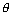 ) & (a sec
) & (a sec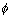 , b tan
, b tan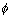 ) is
) is 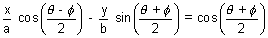
It passes through focus (ae, 0), then
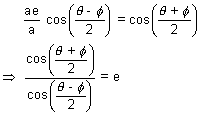
Applying componendo & dividendo we get
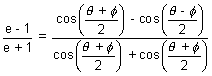
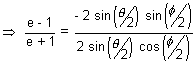

Q.5. Find the locus of poles of normal chords of the rectyangular hyperbola xy = c2.
Ans: Equation of normal at any t is
xt3 - yt = c(t4 - 1) …………………………………. (i)
Lert its ple be P(x1, y1) then the equation of polar is
xy1 + x1y = 2c2…………………………………………….. (ii)
Comparing the coefficients of equations (i) & (ii) as they represent same equation
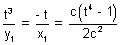
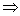 t2 = -
t2 = - 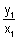 …………………………………………………….. (iii)
…………………………………………………….. (iii)&
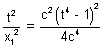 …………………………………………………. (iv)
…………………………………………………. (iv)From (iii) & (iv)
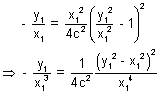
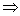 (x12 - y12)2 = - 4c2x1y1
(x12 - y12)2 = - 4c2x1y1Hence locus of (x1, y1) is
(x - y)2 + 4c2xy = 0
Q.6. Find the co-ordinates of the foci & equation of the directrices of rectangular hyperbola xy = c2 ?
Ans: When the hyperbola x2 - y2 = a2 converts into xy = c2 by rotation by - 450 then a2 = 2c2.
So, for
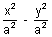 = 1
= 1 Coordinates of foci are (± ae, 0) = (±
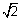 a, 0)
a, 0) Also directrices are x = ±
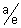 = ±
= ± 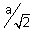
Now we replace
 for (x, y) & 2c2 = a2.
for (x, y) & 2c2 = a2.  Foci =
Foci = 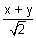 = ± a
= ± a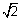 &
& 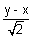 = 0
= 0 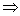 x = y = ± 2a
x = y = ± 2a So Foci are (± 2a, ± 2a)
i.e. (±
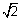 c, ±
c, ± 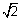 c)
c) Also directrices are
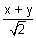 = ±
= ± 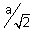
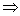 x + y = ± a
x + y = ± a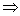 x + y = ±
x + y = ± 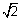 c (
c (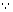 a2 = 2c2)
a2 = 2c2) are the directrices of the rectangular hyperbola.