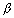Q.7. If the tangent at P of the hyperbola xy = c
2 meets the asymptotes ate L & M & C is the centre of hyperbola. Prove that PL = PM = CP.
Ans:
Let P(ct,
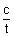
) be any point, then equation of tangent at P is
x + t
2y = 2ct
It meets the asymptotes i.e. x = 0 & y = 0 at L, M respectively.
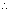
L = (2ct, 0)
& M = (0,
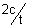
)
Clearly mid point of LM is
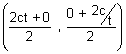
= (ct,
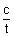
) = P
Therefore PL = PM =
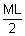
................................................... (i)
& CP =
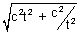
But ML =
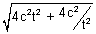
ML = 2
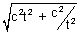
ML = 2CP
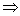
CP =
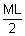
................................................. (ii)
By (i) & (ii)
PL = PM = CP
Q.8. Find the equation of hyperbola whose asymptotes are 2x + y + 2 = 0 & x + y + 3 = 0 & which passes through (0, 1), also find the equation of conjugate Hyperbola.
Ans: We know that the combined equation of asymptotes & hyperbola differ by a constant.
The combined equation of assymptotes is
(2x + y + 2)(x + y + 3) = 0
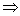
2x
2 + y
2 + 3xy + 8x + 5y + 6 = 0
Then let the equation of hyperbola be
2x
2 + y
2 + 3xy + 8x + 5y + 6 +
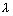
= 0
As it passes through (0, 1) we get
0 + 1 + 0 + 0 + 5 + 6 +
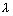
= 0
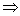
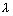
= - 12
Hence the equation of hyperbola is
2x
2 + y
2 + 3xy + 8x + 5y - 6 = 0
We also know that
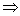
The equation of conjugate hyperbola = 2(combined equation of assymptotes) - (equation of hyperbola)
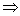
equation of conjugate hyperbola is
2(2x
2 + y
2 + 3xy + 8x + 5y + 6) - (2x
2 + y
2 + 3xy + 8x + 5y - 6)
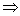
equation of conjugate hyperbola is
2x
2 + y
2 + 3xy + 8x + 5y + 18 = 0
Q.9. If the polars of (x
1, y
1) & (x
2, y
2) with respect to hyperbola
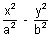
= 1 are at right angles, then show that
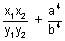
= 0.
Ans: Equation of polar of (x
1, y
1) & (x
2, y
2) with respect to hyperbola
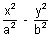
= 1 are
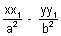
= 1 &
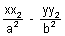
= 1
Therefore the slopes are
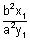
&
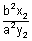
Since the polars are at right angles
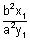
x
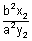
= - 1
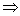
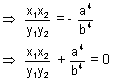
Q.10. Prove that product of perpendiculars from any point on the hyperbola
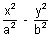
= 1 to its asymptotes is
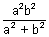
.
Ans: The asymptotes are
y =
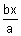
& y = -
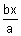
Let the point be P (x
1, y
1)
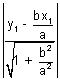
Perpendicular distance from y =
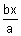
is
L
1 =
Perpendicular distance from y = -
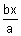
is
L
2 =
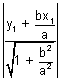
L
1L
2 =
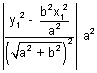
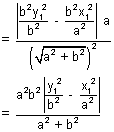
But
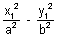
= 1 (x
1, y
1 lies on hyperbola)
L
1L
2 =
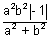
L
1L
2 =
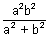
MEDIUM
Q.1. Show that the locus of the centre of circle which touches two given circles externally is a hyperbola.
Ans: Let C
1, C
2 be the centres of the two given circles & p & q be their radii. Let
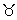
be the radius of the circle touching them externally & c be its centre, then,
CC
1 = p + r
CC
2 = q +
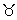
We can see that
CC
1 - CC
2 = p - q = constant
Here we observe that the difference of distances of the centre from two fixed points is constant. Hence it satisfies the property of hyperbola the locus of centre is a hyperbola.
Q.12. Find the locus of mid points mid of the chord of x
2 + y
2 = 16 which are tangets to the hyperbola
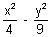
= 1.
Ans: The equation of chord of circle with (h, k) as mid point is
T = S
1i.e. hx + ky - 16 =h
2 + k
2 - 16
hx + ky = h
2 + k
2 .................................................... (i)
If (i) is the tangent to hyperbola therefore it must be of the form
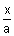
sec
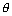
-
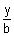
tan
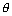
= 1
here a = 2 b = 3
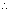
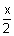
sec
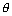
-
tan
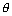
= 1 .................................................. (ii)
Equating coefficients of (i) & (ii)
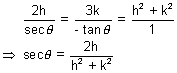
& tan
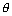
= -
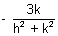
Using sec
2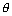
- tan
2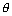
= 1 we get
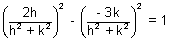
4h
2 - 9k
2 = (h
2 + k
2)
2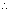
Locus of (h, k) is (x
2 + y
2)
2 = 4x
2 - 9y
2Q.13. A circle with cintre (3
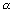
, 2
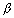
) & of variable radius cuts the rectangular hyperbola x
2 - y
2 = 9a
2 at the points A, B, C, D. Find the locus of centroid of triangle ABC ?
Ans: The equation of circle is
(x - 3
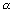
)
2 + (y - 3
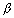
)
2 =
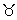 2
2 .................................. (i)
& hyperbola is
x
2 - y
2 = 9a
2 ..................................................... (ii)
Eliminating y from (i) & (ii) we get
4x
4 - 24
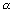
x
3 + .............................. = 0
It is a equation of power four, having roots as x
1, x
2, x
3, x
4.
Let (h, k) be the centroid of PQR
Then,
h =
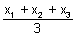
& k =
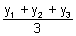
We have x
1 + x
2 + x
3 + x
4 = 6
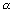
................................. (iii)
& similarly y
1 + y
2 + y
3 + y
4 = 6