Therefore using (iii) & (iv) we get
h =

& k =
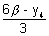
But (x
4, y
4) lies on hyperbola
x
42 - y
42 = 9a
2
9(h - 2
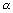
)
2 - 9(k - 2
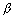
)
2 = 9a
2
(h - 2
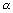
)
2 - (k - 2
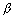
)
2 = a
2Hence the Locus of (h, k) is
(x - 2
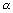
)
2 - (y - 2
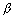
)
2 = a
2Q.14. A normal to the hyperbola
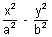
= 1 meets the axes in M & N & lines MP & NP are drawn perpendicular to the axes meeting at P. Find the Locus of P.
Ans:
Equation of normal at Q is ax cos
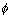
+ by cot
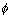
= a
2 + b
2. The normal meets the x-axis at M
M =
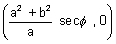
& N =
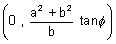
Equating of line MP is
x =
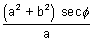
.................................... (i)
& equating of line NP is
y =
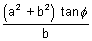
.................................... (ii)
From (i) & (ii)
sec
2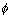
- tan
2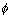
= 1
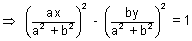
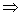
a
2x
2 - b
2y
2 = (a
2 + b
2)
2 is the required Locus of P.
Q.15. A point P moves such that the tangents from it to the hyperbola 4x
2 - 9y
2 = 36 are mutually perpendicular. Find the Locus of P.
Ans: We can write the combined equation of both thetangents. Let P = (
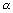
,
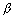
Then, SS
1 = T
2 S< = 4x
2 - 9y
2 - 36
T = 4x
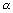
- 9y
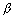
- 36
S
1 = 4
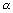 2
2 - 9
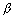 2
2 - 36
Using SS
1 = T
2 (4x
2 - 9y
2 - 36)(4
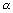 2
2 - 9
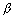 2
2 - 36) = (4x
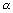
- 9y
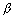
- 36)
2This is an equation of pair of lines, if these are perpendicular
then the coefficient of x
2 + coefficient of y
2 = 0
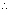
Coefficient of x
2 = - 144 - 36
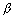 2
2 ............................... (i)
Coefficient of y
2 = 324 - 36
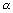 2
2 ................................. (ii)
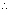
by (i) & (ii)
- 36
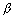 2
2 - 36
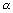 2
2 = - 180
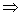
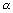 2
2 +
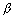 2
2 = 5
Therefore the Locus of (
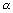
,
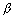
) is x
2 + y
2 = 5
Which is the equation of director circle. Hence we can say that the Locus of point of intersection of two perpendicular tangents is the director circle.
HARD
Q.16. The normals at three points P, Q, R on a rectangular hyperbola intersects at a point T on the curve. Prove that the centre of hyperbola is the centroid of triangle PQR.
Ans: Equation of normal at any point (ct,
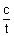
) on xy = c
2 is
xt
3 - yt - ct
4 + c = 0
It will pass through T. So, ht
3 - kt - ct
4 + c = 0 .......................... (i)
Let T = (h, k) & k =
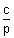
........................................................ (ii)
Curve P is the parameter
By equations (i) & (ii) we get
cqt
3 -
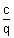
t - ct
4 + c = 0
qt
3 -
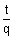
- t
4 + 1 = 0
q
2t
3 - t - qt
4 + q = 0
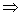
q(qt
3 + 1) - t(qt
3 + 1) = 0
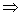
(q - t)(qt
3 + 1) = 0
but q
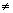
t
qt
3 + 1 = 0 ............................................. (iii)
This is a cubic equation in t representing the points P, Q, R where normals are drawn.
Let the roots be t
1, t
2, t
3 such that
P = (ct
1,
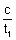
q = (ct
2,
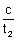
) R = (ct
3,
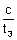
)
From equation (iii) we get
t
1 + t
2 + t
3 = 0 ........................................ (iv)
& t
1t
2 + t
2t
3 + t
1t
3 = 0 ................................. (v)
Now the centroid of Triangle PQR is
x = c(t
1 + t
2 + t
3)
= c(0) (From equation (iv)
= 0
y =
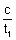
+
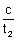
+
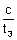
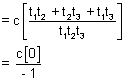
= 0 (From equation (v))
Hence the centroid of
PQR is (0, 0) which is the centre of the given hyperbola.
Dumb Question: Initially we have considered the point 't' & Later use considered t
1, t
2, t
3 so this t is t
1 or t
2 or t
3 ?
Ans: Initially we have written that consider any point 't' which can be either t
1 or t
2 or t
3. If it is t
1, other two are t
2, t
3 & if its is t
2, other two are t
1, t
3 & so on. These three point forms a symmet4ry, therefore t is general, either t
1, t
2 or t
3.
Q.17. The chord of contact of the tangents through P to the hyperbola
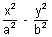
= 1 subtends a right angle at the centre. Prove that the Locus of P is the ellipse ?
Ans: Let the point P be (h, k), then the equation of chord of contact is
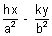
= 1
Now we know that the equations of line passing through origin & the points of intersection of chord of contact with hyperbola is obtained by homogenizing the hyoerbola.
Therefore
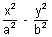
= 1
Can be written as
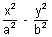
= (1)
2 =
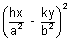
because
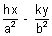
= 1
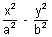
=
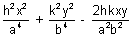
This is a homogeneous equation representing pair of staright lines, if these subtend a right angle at the centre than
Coefficient of x
2 + coefficient of y
2 = 0
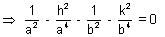
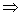
Multiplying by a
4b
4 we get
a
2b
2 - h
2b
4 - a
4b
2 - k
2a
4 = 0
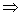
b
4h
2 + a
4k
2 = a
2b
2(b
2 - a
2)
Hence the Locus of (h, k) is
b
2x
2 + a
2y
2 = a
2b
2(b
2 - a
2)
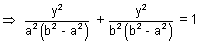
Hence the Locus is an ellipse.
Dumb Question: Why we have homogenised the hyperbola ?
Ans: Let us consider a general curve
ax
2 + 2hxy + by
2 + 2gx + 2fy + c = 0
& any general line lx + my + n = 0
By making the curve homogeneous means
By usig given line make the curve homogeneous of degree 2.
Consider lx + my + n = 0 , then
l =
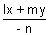
Now consider curve
ax
2 + 2hxy + by
2 +2gx.1 + 2fy.1 +c.(1)
2 = 0
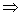
ax
2 + 2hxy + by
2 +2gx
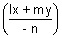
+ 2fy
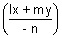
+ c
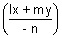 2
2 = 0
Hence this is a curve passing through origin & also homogeneous & because it is obtained by the help of curve & the line it represents the pair ofstaright lines passing through origin & points of intersection of line with the curve.
i.e. of OA & OB.
KEY WORDS
Focus.

Vertex.

Directrix.

Eccentricity.

Latus Rectum.

Absicca.

Ordinate.

Centre.

Axes.

Double Ordinate.

Focal Chord.

Parametric Equation.

Eccentric Angle.

Focal Distance.

Conjugate Hyperbola.

Tangent.

Normal.

Slope.

Pair of Tangents.

Chord of Cantact.

Pole.

Polar.

Diameter.

Conjugate Diameter.

Director Circle.

Asymtotes.

Rectangular Hyperbola.

Locus.

Transverse Axis.

Conjugate Axis.