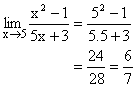limit-continuity-2

Theorem on Limits:

Let 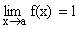and 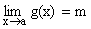. If l and m exist then,

1) .

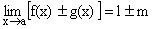2) .

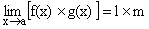3) 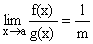Provided m ¹ 0.

4) 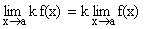Where k is constant.

5) If f(x) £ g(x) then l £ m.

6) .

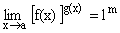7) If f(x) £ g(x) £ h(x) for all x.

 and 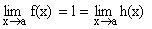then 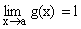(Squeeze play/ Sandwitch Theorem).

Illustration 3:

If [x] denotes the integral part of x, then find .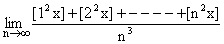

Solution:

Let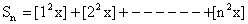

Now we know

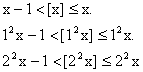
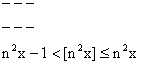
\ Adding them all gives us

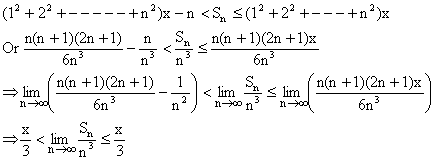
By using squeeze play theorem we get,

.

 

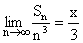Some important expansions (Power Series):

1) .

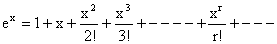2) 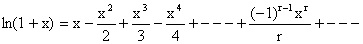  Here -1 < x £ 1.

3) .

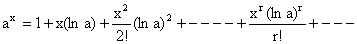4) .

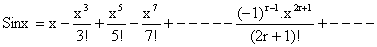5) .

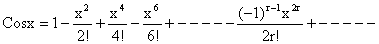6) .

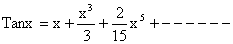7) .

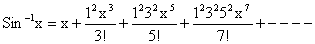8)

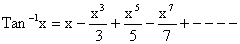
9) 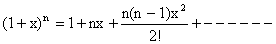(For rational or integral n).

Illustration 4:

Find the series expansion of Sin²x?

Solution:

Now we know that

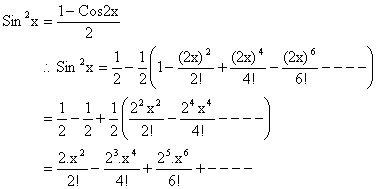
Note that many other series could be found in that way as we found the series for Sin²x.

 

Some Standard results on limits:

1)

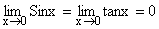
2)

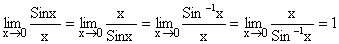
3)

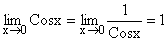
4)

5)

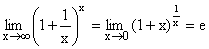
6)

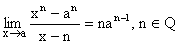
7)

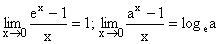
8)

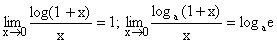
9)

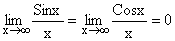
10)

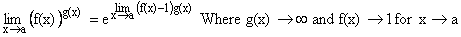
Note: These limits could be derived using the series expansion or by L¹ Hospital’s rule which will discussed in a later section.

Illustration 5:

Find the value of ?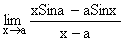

Solution:

 

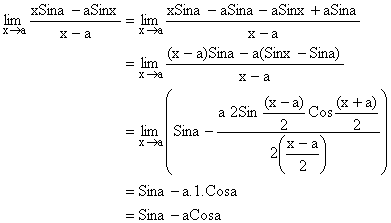
Evaluation of Limits:

1) Direct Substitution:

If we get a finite number by direct substitution of point we are done.

Illustration 6: Find ?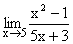

Solution: