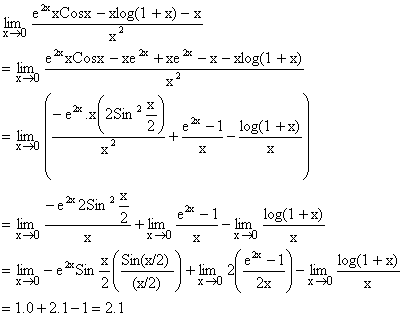limit-continuity-3

2) Algebraic Limits:

A) Factorization process of finding limit.

If direct substitution of x=a in a rational function takes useless form like then a factor of (x-a) can be cancelled from both numerator and denominator. Now again use direct substitution to see if limit can be evaluated.

Illustration 7:

Find ?

Solution:

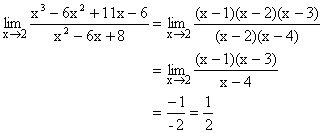
B) Using the result

Illustration 8: Evaluate ?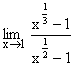

Solution:

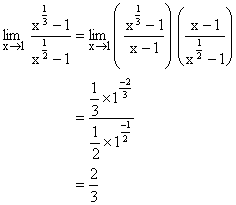
C) Using rationalization:

Some factor which creates form is cancelled by rationalization and limit is evaluated.

Illustration 9: Evaluate ?

Solution:

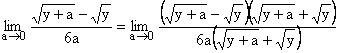
D) Limits where x®

We write down expression as a rational function and then divide each term by highest power of x obtained from numerator and denominator.

Illustration 10: Find the value of ?

Solution:

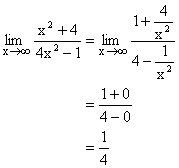
3) Trigonometric Limits:

The trigonometric limits are those which involve trigonometric ratios. The use of the result is a integral part of evaluation of such limits.

Illustration 11: Evaluate ?

= 1´ p ´ 1

= p.

4) Exponential and Logarithmic Limits:

These are the limits which involve use of logarithmic and exponential functions. Some of the standard limits help us in solving these limits.

Illustration 12:

Find the following limits

Solution: