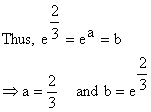limit-continuity-5

PROBLEMS (EASY TYPE)

1) Prove that

Solution:

And so assumes the indeterminate form 0/0 when x tends to 0.

We know for

Sinx < x < Tanx

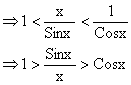
This is true for x>0, the same holds when x<0 in that Sin (-x)/ (-x) = and

Cos (-x) = Cosx.

Now since , it follows from sandwitch theorem,

.

2) Find the value of .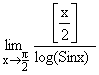

Solution: As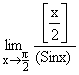

\

Where

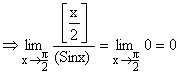
3) Evaluate .

Solution:

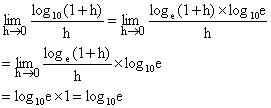
4) Evaluate .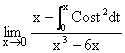

Solution:

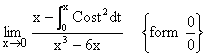
Applying L-Hospital’s Rule we get,

5) Find .

Solution:

For both the numerator and denominator are 0.

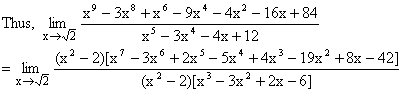
Given [x²-2 ¹ 0].

6) If 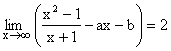then find the values for a and b.

Solution:

We have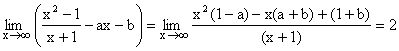

Since, limit of above expression is a finite non-zero number.

\ degree of numerator = degree of denominator

Þ 1-a = 0 Þ a = 1

\ Putting a = 1 in above limit we get

Þ - (1+b) = 2 Þ b = -3

Hence a = 1 and b = -3.

7) Let

Determine a and b such that f(x) is continuous at x=0.

Solution:

Since f(x) is continuous at x=0.

Therefore R.H.L = L.H.L = f (0)

R.H.L at x = 0.

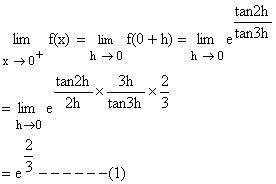
Again L.H.L at x = 0

And f (0) = b ------ (2)