limit-continuity-6

8) A function is defined as follows,

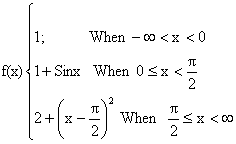
Discuss continuity of f.

Solution:

Continuity at x = 0

L.H.L at x = 0

R.H.L at x = 0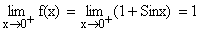

f (0) = 1+Sin0 = 1

= L.H.L = R.H.L = f (0) so f (x) is continuous at x = 0.

Continuity at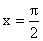

L.H.L at =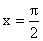

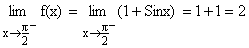
R.H.L at =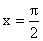

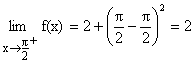
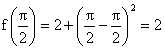
\ R.H.L = L.H.L =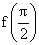

So, f(x) is continuous at .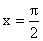

Hence f(x) is continuous over the whole real number.

9) Discuss the continuity of the function:

g (x) = [x] + [-x] at integral values of x.

Solution:

Here x can assume two values a) Integers b) Non-Integers

a) If x is an integer

[x] = x and [-x] = -x Þ g(x) = x-x = 0.

b) If x is not an integer.

Let x = n+f Where n is an integer and f Î (0, 1).

Þ [x] = [n+f] = n.

Þ [-x] = [-n-f] = [(-n-1) + (1-f)] = (-n-1).                   (Because 0<f<1 Þ (1-f) <1)

Hence g(x) = [x] + [-x] = n + (-n-1) = -1.

So we get;

g(x) = 0; if x is an integer

    = -1; if x is not an integer

Let us discuss the continuity of g(x) at a point x=a (Where a Î integer).

L.H.L = 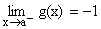(as x®a^-, x is not an integer)

R.H.L = 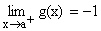(as x®a⁺, x is not an integer)

But g (a) = 0 because a is an integer.

Hence g(x) has a removable discontinuity at integral values of x

\ g (x) = [x] + [-x], xÏ integer.

            = -1,            x Î integer.

10) Let f(x) = x- |x-x²|, -1£ x £ 1. Discuss the continuity of f(x) in the closed interval

[-1, 1]. Draw the graph of f(x) in that interval.

Solution:

Here f(x) = x-|x (1-x)|

= x- |x| |x-1|, -1£ x £ 1.

Now using definition of modulus function we have

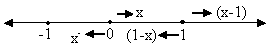
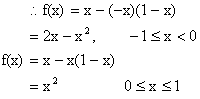
We know that polynomials are continuous every where, so only doubtful point is the turning point x=0 of definition.

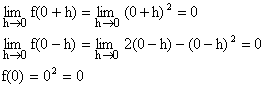
So f(x) is continuous at x=0.

Hence f(x) is continuous in [-1, 1].

Hence the graph of f(x) is continuous in [-1, 1] and

f (x) = 2x-x² in -1£ x < 0

x² in 0£ x £ 1.

\ The graph of f(x) is as follows;

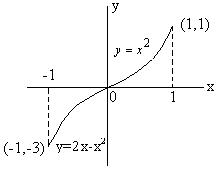
11) A function f(x) is defined by

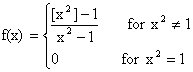
Discuss the continuity of f(x) at x=1.

Solution:

We have

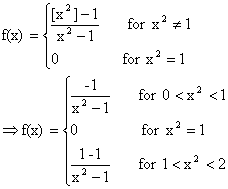
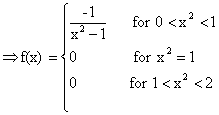
\ R.H.L at x² =1

Þ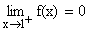

Also L.H.L at x²=1

Þ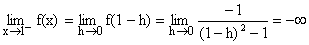

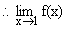does not exist {as R.H.L ¹ L.H.L}

Hence f(x) is not continuous at x=1.