limit-continuity-8
5) Find the point of discontinuity of ![]() where
where ![]() .
.
Solution:
The function ![]() is discontinuous at the point x=1 ----- (1)
is discontinuous at the point x=1 ----- (1)
The function ![]() is discontinuous at u=-2 and u=1.
is discontinuous at u=-2 and u=1.
When u = -2, ![]()
![]()
Hence composite function y = g(x) is discontinuous at three points ![]() .
.
6) If ![]() examine the continuity of f(x) at x=1.
examine the continuity of f(x) at x=1.
Solution:
To examine the continuity at x=1, we are required to derive the definition of f(x) in the intervals x<1, x>1 and at x=1, i.e. on and around x=1.
Now if 0<x<1
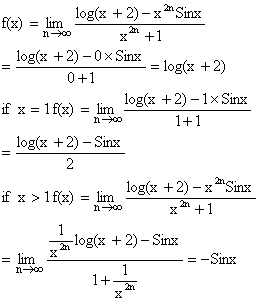
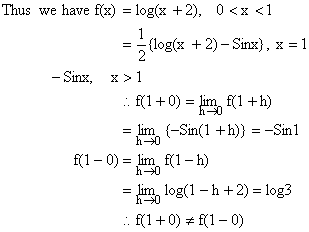
So f(x) is not continuous at x=1.
Dumb Question:
1) How does ![]() varies with the value of x?
varies with the value of x?
Ans: Now suppose x<1
So, ![]()
\ ![]() =0
=0
If x =1 then ![]()
If x>1 then ![]()
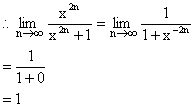
7) Show 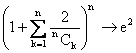 as n®
as n® ![]() (for n ³ 6)
(for n ³ 6)
Solution:
Let ![]() while for n ³ 6.
while for n ³ 6.

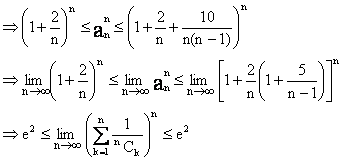
\ By squeeze principle for limits,
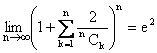 .
.
Ø Limit
Ø Extending / Approaching
Ø Right Hand Limit
Ø Left Hand Limit
Ø Infinity ![]()
Ø Sandwitch Theorem / Squeeze play Theorem.
Ø Power Series
Ø L-Hospital’s Rule
Ø Continuity
Ø Removable discontinuity
Ø Irremovable discontinuity