study material-mathematics-algebra-logarithms
Logarithms - 2
- loga(m/n) = logam - logan
Why ?
Let logam = x
logan = y
m = ax and n = ay [Using definition]
m/n = ax/ay = ax - y
=> logam/n = x - y
= logam - logan
- logamn = n logam.
why ?
Let logamn = y
By definition ay = mn
or, ay/x = m
Again using definition of log
logam = y/x
or n logam = y
so, logamn = n logam.
Illustration - 2. If log1227 = a, then log316 = ??
log316 = log324 = 4 log32 ……………………………………….. (i)
Now, log1227 = log1233
= 3 log123
=
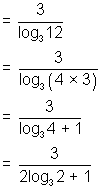
So, log32 =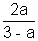
Now, log3 =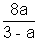
*7. log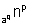
= logan
log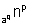 = p logaqn - (Using formula 6.)
= p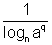
- (Using formula 3.)
=
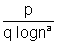- (Using formula 6.)
=
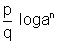- (Using formula 3.)
*8.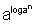
= n
Illustration - 3.
Evaluate.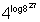
=
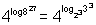
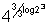(Using formula 7)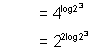
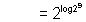(Using formula 6)
= 9 (using formula 8)
Hence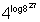 = 9
logpa > logpb
=> a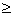
b if p is greater than 1 i.e. p > 1
or b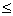
a if p is positive and less than 1, 0 < p < 1
Remembering Tip:- If base if > 1 then inequality remains same and if base is + ve but less than 1 then sign of inequality is reversed.
Why ?
Let logpa = x
logpb = y
So, a = px
and b = py
Now x > y is given
So, if p > 1
then a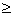 b
and if 0 < p < 1
then a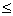 b