Logarithms - 3

Illustration - 4.
If log_0.2(x - 1) < log_0.4(x - 1) then x lies interval.
Now, log_0.2(x - 1) <
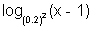
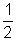
=> log_0.2(x - 1) < log_0.2(x - 1)
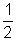
=> log_0.2(x - 1) < 0
or, log_0.2(x - 1) < 0 = log_0.21
Since 0.2 is less than 1 so, x - 1 > 1 or x > 2

log - flow Questions
Easy
Q1. Find the value of log₈128 ?
Ans:- log₈128 =
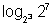
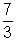
                      = log₂2
                      =

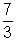
Q2. What is the approx vaslue of log₁9.903 ?
Ans:- The value does not exist because the base of a logarithm cannot be 1.

Q3. Find solution of the equation ?
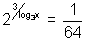
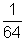
Ans:- = 2^{- 6}
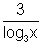
So, = - 6
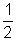
- = log₃x
So, x =

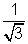
Q4. Find equation log_ex + log_e(1 + x) = 0 free from log ?
Ans:- log_ex + log_e(1 + x) = 0
=> log_e(x(1 + x)) = 0
So, x(1 + x) = 1
or, x² + x + 1 = 0

Q5. If log₂x  X  log₂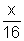 + 4 = 0 then find the value of x.
Ans:- log₂x  X  (log₂x - log₂16) + 4 = 0
=> (log₂x)² - 4 log₂2 log₂x + 4 = 0
=> (log₂x)² - 4 log₂2 + 4 = 0
=> (log₂x - 2)² = 0
=> log₂x = 2
or, x = 4.

Q6. If 2 log₈N = p, log₂2N = q and q - p = 4 then find the value of N ?
Ans:-      p = 2 log₈N
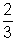
                 = log₂N
              q = log₂2N
                 = log₂2 + log₂N
                 = 1 + log₂N
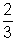
        q - p = 1 + log₂ N - log₂N
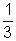
                 = 1 + log₂N = 4 (Given)
So, log₂N = 9
0r N = 2⁹ = 512

Q7. If a, b, c are consecutive positive integrals and log(1 + ac) = 2K then find value of K ?
Ans:- Let a = n
         b = n + 1
         c = n + 2
So, log(1 + ac) = log(1 + n(n + 2))
                        = log(1 + n² + 2n)
                        = log(n + 1)²
                        = 2 log(n + 1)
                        = 2 logb
Value of K is logb.

Q8. Find value of x if log₃x.log_y3.log₂y = 5 ?
Ans:-   log₃x.log_y3.log₂y = log₃x.log₂3
                                      = log₂x
                                      = 5 (Given)
So, x = 2⁵ = 32.

Q9. The value of e^{ln(ln 7)} IS 7, True or false.
Ans:-   e^{ln(ln 7)} = ln 7^{ln e}
                       = ln 7
So, it is false.