Logarithms - 4

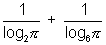
Q10. The value of is greater then 2. true or false ?
Ans:-
                                     =
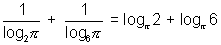
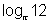
Now, 1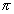2 > ²
So,
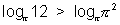
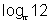
or > 2
So, It is true.

Logarithms - flow Questions
Medium
Q1. If a, b, c are distinct positive numbers each different from 1 such that
[log_ba log_ca - log_aa] + [log_ab log_cb - log_bb] + [log_ac log_bc - log_cc] = 0 then find the value of abc ?
Ans:- Let us change all logarithms to base
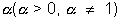
So, the eqⁿ now becomes
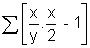
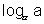
= 0 where x = etc.
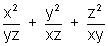
So, = 3
or, x³ + y³ + z³ - 3xyz = 0
or, (x + y + z)(x² + y² + z² - xy - yz - zx) = 0
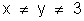
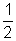
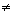
Since we have,     x² + y² + z² - xy - yz - zx = [(x - y)² + (y - z)² + (z - x)²] 0

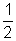
** Tip: Writing x² + y² + z² - xy - yz - zx   as [(x - y)² + (y - z)² + (z - x)²] which is non-negative for real x, y, z is an useful magnipulation is solving many questions.
So, we calculate x + y + z = 0 that is
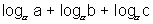
= 0
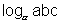
or, = 0
or, abc = 1

Dumb Question:- Why x² + y² + z² - xy - yz - zx is not equal to 0 ?
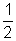
Ans:- x² + y² + z² - xy - yz - zx = [(x - y)² + (y - z)² + (z - x)²]
Now since it is given in question that x, y, z are distinct positive numbers, this cannot be equal to zero.

Q2. If log_a(ab) = x, then find value of log_b(ab) ?
Ans:- log_a(ab) = log_aa + log_ab = 1 + log_ab = x
So, log_ab = x - 1
or log_ba =
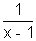
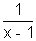
or, log_ba + log_bb = + 1
=> log_b(ab) =
                   =

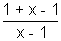
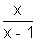
Q3. Find the least value of the expression
2 log₁₀x - log_x(0.01) for x > 1
Ans:- 2log₁₀x = log_x(0.01)
                     = 2 log₁₀ x - log_x10^-2
                     = 2(log₁₀x + log_x10)
                     = 2(log₁₀x + )
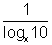
                     = 2
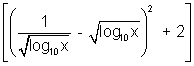
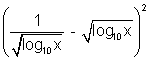
                     = 2 + 4
So, the minimum value is 4.