Logarithms - 5

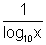
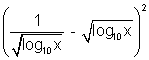
Dumb Question:- How does log₁₀x + was equated to + 2 ?
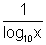
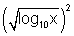
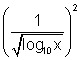
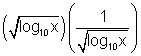
Ans:-   log₁₀x + = + - 2 + 2
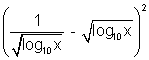
                                     = + 2
Since x is given to be > 1. So, log₁₀x is a positive no.

Q4. Solve log_{2x + 3}(6x² + 23x + 21) = 4 - log_{3x + 7}(4x² + 12x + 9)

Ans:- log_{2x + 3}(6x² + 23x + 21) = 4 - log_{3x + 7}(4x² + 12x + 9)

=> log_{2x + 3}[(2x + 3)(3x + 7)] = 4 - log_{3x + 7}(2x + 3)²

=> 1 + log_{2x + 3}(3x + 7) = 4 - 2 log_{3x + 7}(2x + 3)

      log_{2x + 3}(3x + 7) = 3 -

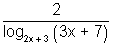
Let log_{2x + 3}(3x + 7) = y

      y = 3 -
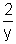
      y² - 3y + 2 = 0
=> (y - 1)(y - 2) = 0
So, y = 1, y = 2
So, log_{2x + 3}(3x + 7) = 1

=> 3x + 7 = 2x + 3
=> x = - 4
But, this means that 2x + 3 = - 5 is a -ve value and base cannot be -ve. So, y = 1 is ruled out.
So, Now let us test y = 2
      log_{2x + 3}(3x + 7) = 2

=> (2x + 3)² = 3x + 7
      4x² + 12x + 9 - 3x - 7 = 0
      4x² + 9x + 2 = 0
=> x = - 2, -
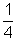
Following similar argument as above x = -2 is rule out, So, the final solution is x = -

Dumb Question:- Why x = -2 solⁿ was ruled out ?
Ans:- If x = -2 then 2x + 3 = -1.
Again, the base cannot be a -ve no, so x = -2 is ruled out.

**Tip :- Never obtain a solⁿ and believe it is a solution, always try and cross check or other way could be that you write conditions which solⁿ should satisfy while solving the question itself definitely - a cleaner aproach.

Q5. Find the value of x satisfying the equation.
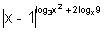
= (x - 1)⁷ ?
Ans:- L.H.S. is a positive no being an exponential.
So, R.H.S. should also be +ve.
R.H.S. will be +ve if x > 1 and in that case |x - 1| = x - 1.
Hence, we can write given eqⁿ as
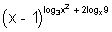
= (x - 1)⁷
This gives log₃x² - 2 log_x9 = 7
Now if log₃x = y, then eqⁿ reduces to
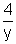
     2y - = 7
or, 2y² - 7y - 4 = 0
or, y = 4, -
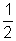
or, log₃x = 4, -
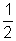
=> x = 3⁴, 3 ^-
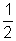
Since x > 1 so, x = 3 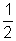^{- is rejected.
Hence x = 81}