Null Matrix :-
MAtrix with all elements O.
Transpose of a Matrix:- The matrix obtaired from a given matrix A, by inter changing rows and columns is called transpose of A and is denoted by a
T . or A
1.
Properties of Transpose (Secondary In formation):-
(i) (A
T)
T = A
(ii) (A + B)
T = A
T + B
T
(iii) (
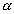
A)
T =
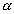
. A
T
(iv) (A B)
T = B
T A
T.
Conjugate of a Matrix:- A matrix obtained from any given matrix A coutaining complex number as its elements, or replaing its elements by the corresponding conjugate complex no is called conjugate of A and is denoted by
.
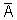
Properties of conjugate (Secondary Information:-
(i)
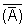
= A
(ii)
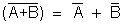
(iii)
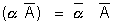
(iv)
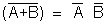Transpose Conjugate of a Matrix:-
The transpose of conjugate of a matrix denoted by
.
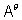
Properties of Transpose of conjugate:-
(Secondary Information):-
(i)
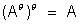
(ii)
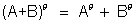
(iii)
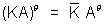
(iv)
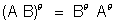ALGEBRA OF MATRICES:-
Addition and Subtraction:- Any two matrices can be added lif they are of same order and the (or Subtrected)
resulting matrix is of same order, corresponding elements are added or subtracted .
Scalar Multiplication:-
The matrix obtained by multiplleying every element of by a scalar
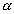
is called the scalar multiple of A by
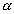
and is denoted by
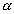
A .
Multipliecation of Matrices:-
Two matrices can be multiplied lonly when the no of columns in the first is equal to the no . of rows inm the second. Such matrices are called conformable for multiplication.
If A B = c
A - [a
ij]
mXn B - [b
ke]
nXp
C
ij2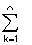 
a
ik b
kj
Special Matrices (Secondary Information:-
Symmetric and Skew Symmetric Matrices:-
A square matriex is A is said to be symmetric if
A = A
T.
and skew symmetric if A = - A
T.
Unitary Matrix
A matrix is unitary if
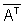
A = 1