Matrices & Determinants - 3

Hermition and skew - Harmition Matrix :-

A square matrix is said to mermition if A = .
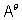
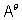
and skew Hermition if = - A .

Singular Matrix :- Ahy square matrix A is singular if | A | = O .

Orthogonal Matrix :- Any squrae matrix A of order n is said to be orthogonal if A A^T = A^T A = I_n.

Idempotent Matrix :- A square matrix is called idmpotent provided it satisfies the selation A² = A .

In volutary Matrix :-

A matrix such A ² = I .

Nilpotent Matrix

A square matrix such that A ^m = O where m is Q posetive integer .

Adjoint of a Square Matrix
Let A be a square matrix of order n and let C_ij ;be cofactor of a_ij in A. Then the transpose of the matrix of cofacturs of elements of A is called the adjoint of A and is denoted by adj A .

We have
A (adj A) = | A | I_n = (adj A) A

Onverse of a Matrix
A no n - singular square matrix of ordere n is invertible if there exists a square matrix B of the same order such that AB = I_n = BA .

A^-1 = B
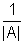
A^-1 = adj A .

properties of inverse of a matrix :-

(Secondary Information).

(i) (A B)^-1 = B^-1 A ^-1

(ii)(ABC ........ ) ^-1 = ........C^-1 B^-1 A^-1

(iii) (A^T) ^-1 = (A^-1 )^T

(iv) A is a no n - singular matrix of order n . There |adj A| = |A| ^1-n

(v) (A B) = adj B . adj A .

(vi) A is are invetible square matrix . There
adj (A^T) = (adj^-A)^T

(vii) If A is a no n - singular square matrix, there
adj(adj^-A) = |A|^n-2 A .

System of Simultaulons Linear Equations :-
a₁₁ x₁ + a₁₂ x₂ + ....... + a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ + ....... + a_2n x_n = b₂


a_n1 x₁ + a_n2 x₂ + ....... + a_nnx_n = b_n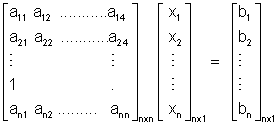



AX = B
X = A^-1 B

(i) If A is non singular, the system of equation AX = B has a uonique so1⁴ given by X = A ^-1 B .

(ii) If A is singular and (adj A) B = O, there system of equation given by AX = B is cousistent with. Infinefely many solutions.

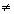
(iii) If A is a singular matrix,and (adj A) . B O, then the system of equation given by AX = B is inconsestent .