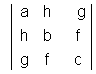Properties of determinants (Secondary Information) :-
1. If rows be changed into columns and columns into the rows, the determinant remain unaltered .
2. If any two rows or columns of a determinant are interchanged the resulting determinant is the negative of the original determinant .
3. If two rows (or ltwo columns) in a determinant have corresponding entries that are equal, the value of the determinant K, then determinant is multiplied by K .
4. If each of the entries in a row (or column) of a determinant is multiplied by K, then determinant is multiplied by K .
5. If each entry in a row (or column) of a determinant is written as the sum of two or more trems than the determinant can be written as the sum of two more determinants .
6. If to each element of a line (row or column) of a determinant be adeled the equimultiples of the corresponding elements of one or more parallel lines, the determinant remains unaltered .
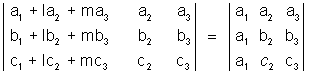
7. If each entry in any cow (or column) of determinant is zero, then the volue of detrminant equal to zero .
8. If determinant varishes for X = a, then (X - a) is a factor of D .
Product of two Determinants :-
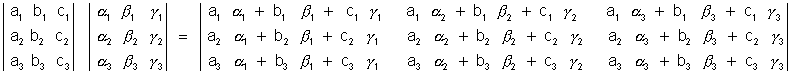Differentiation of a determinant (Sexondary Information) :-
(X) =
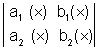
then
(X) =
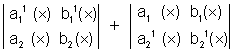
Similarly if
(X) =
, then
1 (X) =
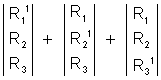Summation of Determinants :-
(Secondary Information)
Let
r =
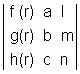
Then
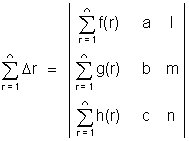Integration of Determinants (Secondary Information ) :-
(X) =
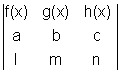
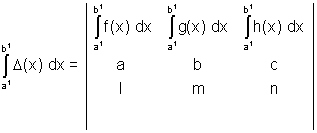Special Determinants (Secondary Information) :-
1. Symmetric Determinant :-
The elements situted at equal distance from the diagonal are equal both in magnitude and sign.
eg.
