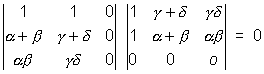Skew symmetric determinant :- Determinant of skew symmetric matrix .
3.
Circulant :- The elements of the rows (or columns) are in cyclic arangements .
eg .
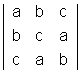Solution of system of Linear Equations :-
a
1X + b
1 y + c
1 z = d
1
a
2X + b
2 y + c
2 z = d
2
a
3X + b
3 y + c
3 z = d
3.
D =
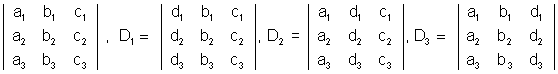
X = D1/D Y = D2/D Z = D3/D
The following cases arise
(1) D
O, the system has one unique solution .
D = O, D
1, D
2, D
3 O, then system is incories tant .
(2) D
1 = O, and D
1 = D
2 = D
3 = O, then the system has infinite solutions .
Illustrations
Q 1. Without expanding, show taht
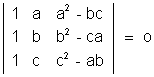Solution :- L H S =
=
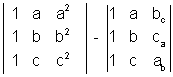
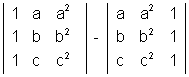
[ R
1
a R
1, R
2 b R
2, R
3 c R
3 and abc taken common]
=
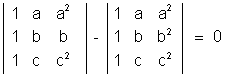
Q 2. Prove that
=
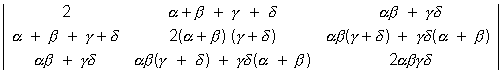
Solution : L H S :-
