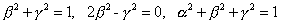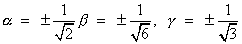Matrices & Determinants - 7

EASY
E 1. If a₁b₁ c and d are real constants and A

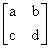
= ,prove that A² - (a + b)A + (ab - bc) I = 0

Sol :- A ² =

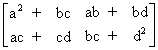
A² = A² - (a + b) A + (ab + bc)I

=

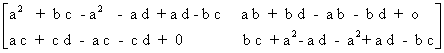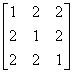
E 1 A = show taht A ² 4 A - 5 I = o

SOl :- A ² =

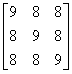
A² - 4 A - 5 I =

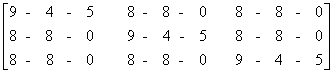
E 3. Solve syste the equation .
X + 3y - 2z = 0., 2x - x - 4z = 0, x - 11y + 14z = 0
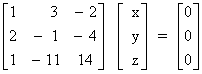
Sol :- => A X = B .


|A| = 0

Solving the terme of z .
x = .


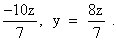
=> x = - 10 k , y = 8 k , z = 7 K
E 4 . For what value of x, the matrix

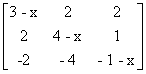
A = is singular .

Solution :- | A | = 0

=> x [(3 - x) (1 + x - 4) - 0 + 2 (2 - 2) ] = 0

x (3 - x) (x - 3) = 0 img x = 0, 3
E 5 :- Evaluate

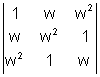Sol :- Applying c¹ 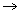c₁ + c₂ c₃

=

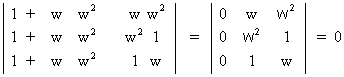E 6 :- For what value of K do the following homogenous system of equations passes a row trivial solution .

x + ky + 3z = 0

3x + ky - 2z = 0

2x + 3y - 4z = 0

Sol :- D = 0
D =

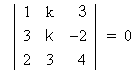
R₁ - 3R₁ and R₃ - 2R₁

=>

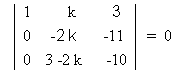
k = 33/2

E 7. Evoluate

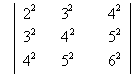Sol :- R₂ - R₁, R₃ - R₂ then C₂ - C₁ and C₃ - C₂

D =

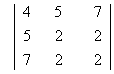
c₃ - c₂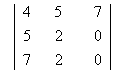

= 2 [ 10 - 14 ] = - 8

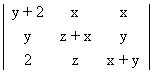
E 8. If = K X Y 2 , Find K .

Solution :- Putting x = 1, y = 1, z = 1 [As if in true for any volues of x₁ y₁ z₁

k = 4

MEDIUM
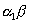
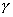
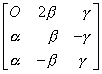
M 1. Determine and if is or thogonal

Solⁿ:- AA¹ = 1

=>

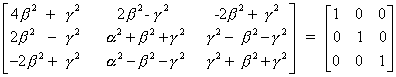
=> 4