Matrices & Determinants - 9

M 2. Using elementary row trans formations find the inverse of the matrix A =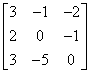

Solⁿ :- A = I A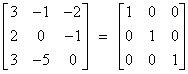
A

. R₁ R₁ - R₂

. R₂ - 2R₁ and R₃ R₃ - 3R₁

. R₂ 1/2 R₂

. R₁ R₁ + R₁ and R₃R₃ + 2R₂

. R₃ 1/2 R₃ and .R₁ R₁ + 1/2 R₃ and R₂R₂ - 1/2 R₃

We get :-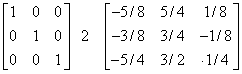
A

A ^-1 =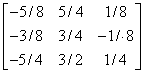

M 3 If a, b and c are P^th1 q^th and r^th terms of are
H.P., prove taht 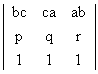= 0

Solution :- A : First term, D : Common difference
1/a = A +(p -1) D, 1/b = A +(q - 1) D, 1/c = A + (r - 1)D

abc

R₁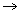R₁ - D R₂ - (A - D)r ,

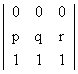= abc = 0

M 4 . for what valume of m, does the system of equation 3x + my - mand 2x - 5y = 20 lhas a solution satisfying the condstion. x > 0, y > 0.

Solution = = 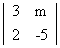- (15 + 2_m)

₁ = - 25m 2 = 60 - 2m

X =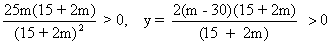

=> m > 30 or m < -15/2