Newtons Law of Motion -4 ( pseudo forces )

CONCEPT OF PSEUDO FORCE:

The Newton ’s Law of motion does not apply in non inertial frame of reference. So a modification is done in order to apply same law in non inertial frames also!

Dumb Question:

<!--[if !supportLists]--> 1)      How the Newton ’s Law is not valid in non inertial frame?

Ans: Suppose there are two observers A and B. A moving with acceleration ‘a’ while B at rest.

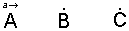
There is another box kept at point C.

Now in frame of reference of B (fixed) which is inertial frame, no force acts on C and hence its acceleration is zero.

But in frame of reference of A (acceleration) which is non inertial frame, C moves towards A with acceleration ‘a’ though there is no force on C.

METHOD OF MODIFICATION IS:

<!--[if !supportLists]--> 1)      Identify the system and mark all forces.

<!--[if !supportLists]--> 2)      Draw FBD of all components.

<!--[if !supportLists]--> 3)      Identify the component that is in a non inertial frame (acc= a₀) and add a ‘pseudo force’ with magnitude = ma₀. Where m is mass of component and a₀ is acceleration of frame and direction opposite to that of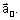

<!--[if !supportLists]--> 4)      Solve the equation using Newton ’s law incorporating the pseudo force.

Illustration:

(Solved example 10 page 75 HCV)

A particle slides down a smooth inclined plane of elevation q, fixed in an elevator going up with an acceleration a₀ as shown in figure (22). The base of the incline has a length L. Find the time taken by the particle to reach the bottom.

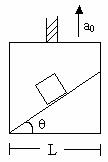
       Fig (22)

Solution:

Let us work in the elevator frame A pseudo force ma₀ in the downward direction is to be applied on the practical of mass m together with the real forces, thus the forces on m are as in figure.

          

<!--[if !supportLists]--> 1)      N normal force

<!--[if !supportLists]--> 2)      mg downward (by the earth)

<!--[if !supportLists]--> 3)      ma₀ downward (by pseudo)

Let ‘a’ be the acceleration of the particle with respect to the incline. Taking components of the forces parallel to the incline and applying Newton ’s law,

mgSinq + ma₀Sinq = ma.

Or a = (g+a₀) Sinq.

This is the acceleration with respect to the elevator. In this frame, the distance traveled by the particle is  Hence,

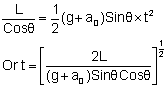
                                                PROBLEMS (EASY TYPE)

1) 6m long ladder weighting 30Kg rest with its upper end against a smooth wall and lower end on rough ground. What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60⁰ with the horizontal without slipping? Take g = 10m/s².

Solution:

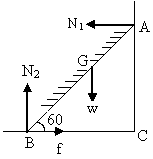
              Fig (23)

AB is a ladder of weight w which acts at its center of gravity G.

ÐABC = 60⁰.

\ÐBAC = 30⁰.

Let N₁ be the reaction of the wall and N₂ the reaction of the ground. Force of friction f between the ladder and the ground acts along BC.

For horizontal equilibrium f = N₁                                             --------------- (1)

For vertical equilibrium N₂ = w                                               ---------------- (2)

Taking moments about B we get for equilibrium

N₁ (6Cos30⁰) – w (3Cos60⁰) = 0                                          ---------------- (3)

Here w = 30´10 = 300N

Solving these equations we get

N₂ = 300N

2) A block of mass 200kg is set into motion on a frictionless horizontal surface with the help of frictionless pulley and a rope system as shown in figure (24). What horizontal force F should be applied to produce in the block an acceleration of 1 m/s²?

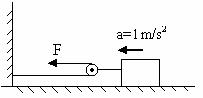
                 Fig (24)

Solution:

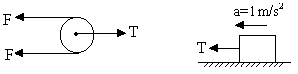
As shown in figure when force F is applied at the end of the string, the tension in the lower part of the string is also F. If T is the tension in string connecting the pulley and the block then,

T = 2F

But T = ma = (200) (1) = 200N

\ 2F = 200N

Or F = 100N

3) Two bodies of masses m₁ and m₂ are connected by a light string going over a smooth light pulley at the end of an incline. The mass m₁ lies on the incline and m₂ hangs vertically. The system is at rest; Find the angle of incline and the force excerted by the incline on the body of mass m₁.

         Fig (25)

Solution:

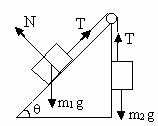
Situation is shown in figure. Taking the body of mass m₂ as the system the forces acting on it are,

<!--[if !supportLists]--> 1)      m₂g vertically downward (by the earth)

<!--[if !supportLists]--> 2)      T along the string up the incline (by the string)

As the system at rest, these forces should add to zero.

This gives, T = m₂g                                                                          ------------- (1)

Consider the body of mass m₁ as the system. The forces acting on it are

<!--[if !supportLists]--> 1)      m₁g vertically downward (by the earth)

<!--[if !supportLists]--> 2)      T along the string up the incline (by the string)

<!--[if !supportLists]--> 3)      N normal to the incline (by the incline)

As the string and the pulley are all light and smooth the tension in the string is uniform everywhere. Hence same T is used for the equations of m₁ and m₂. As the system is in equilibrium these forces should add to zero.

Taking components parallel to the incline.

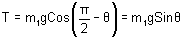                                                     --------------- (2)

Taking component along normal to the incline,

N = m₁gCosq                                                                              --------------- (3)

Eliminating T from (1) and (2)

m₂g = m₁gSinq

Or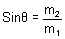

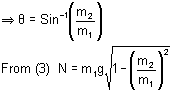
4) A 4kg block is attached to a vertical rod by means of two strings. When the system rotates about the axis of the rod, the strings becomes taunt as shown in figure (26).

a) How many revolutions per second must the system make in order that the tension in the upper cord shall be 60N?

b) What is the tension in the lower cord? (g = 10 m/s²).

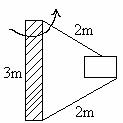
         Fig (26)

Solution:

Let w be the angular velocity of rotation of rod.

Along vertical

T₁Cosq = mg+ T₂Cosq                                                      ------------- (1)

Net force towards center (centripetal force)

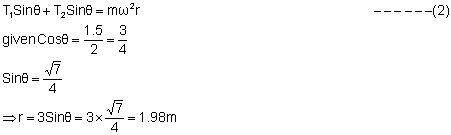
Substituting the values of Cos q, Sinq, r and T₁ = 60N, m= 4Kg in (1) and (2) we get

w = 2.35 rad/sec

T₂ = 6.66N.