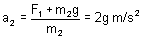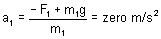5) CONSTRAINT MOTION:
<!--[if !supportLists]--> A) Due to inextensible taut strings.
<!--[if !supportLists]--> B) Due to normal reactions.
A) Due to inextensible taut strings:
As the length of the string is constant, so velocity, components of its ends along the string are equal.
B) Due to normal reactions:
The bodies in contact do not have any relative motion in the normal direction. Relative motion can occur only in perpendicular to normal direction.
Illustration 1:
A) Find m if B moves as shown in figure (6).
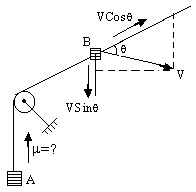
Fig (6)
Solution:
The ‘V’ is broken down into two components – along the perpendicular to string and parallel to string. Now from the above principle mVCosq. (Ans).
B)
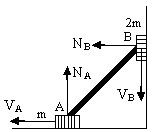
Fig (7)
A and B are attached using a rod. Now motion occurs in the direction perpendicular to normal direction as shown.
Tip: Remember the following rules:
<!--[if !supportLists]--> 1) Velocity components along a string are equal.
<!--[if !supportLists]--> 2) No motion (relative) occurs in normal direction.
<!--[if !supportLists]--> 3) Acceleration component in normal direction are equal.
Illustration 2:
Example 5.20 page 190 D C Pandey
Find the Constraint relation between a1, a2, and a3.
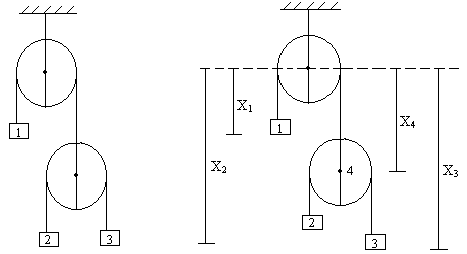
Fig (8)
Solution:
Points 1, 2, 3, 4 are movable let their displacements from a fixed line be x1, x2, x3, and x4.
We have x1+x4 = l1 (length of first string) ---------------- (1)
And (x2 – x4) + (x3 – x4) = l2 (length of second string)
Or x2 + x3 – 2x4 = l2 ----------------- (2)
Or double differentiating with respect to time we get
a1 + a4 = 0 ------------------- (3)
a2 + a3 – 2a4 = 0 ------------------ (4)
But since a4 = -a1 from equation (3)
We have a2 + a3 + 2a1 = 0
This is the required constant relation between a1, a2, and a3.
Dumb Question:
<!--[if !supportLists]--> 1) Why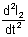 
and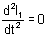 
?
Ans: If the rope is given inextensible then l2 and l1 does not change with time. So their derivatives are zero.
Illustration 3:
In the adjacent figure (9) mass of A, B and C are 2kg, 5kg, and 4kg respectively. Find
A) Acceleration of the system.
B) Tension in the string. Neglect friction (g = 10 m/s2)
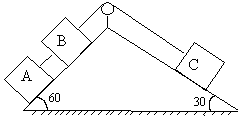
Fig (9)
Solution:
A) Take A+B as whole system then,
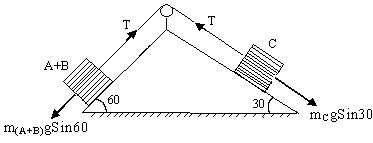
7gSin60 – T = 7a
T – 4gSin30 = 4a
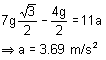
B) For the tension in the string between A and B
FBD of A-
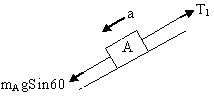
Fig (10)
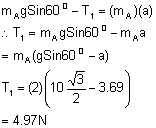
For the tension in the String between B and C
FBD of C-
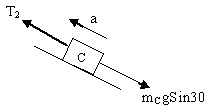
Fig (11)
Tip: Always remember that the two end string over a pulley; always move up and opposite velocities with respect to pulley only.
6) SPRINGS:
Hook’s law for ideal springs Fsp = -Kx
Where, K ® Spring constant
x® elongation
Dumb Question:
<!--[if !supportLists]--> 1) What is the force applied on wall in a situation like:
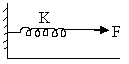
Ans:
Let the force applied be equal to F1 then FBD of spring:
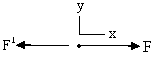
So F – F1 = ma
Now since we are considering light springs, m®0
So, F1 = F
Hence the force applied by a light spring on connecting bodies at both ends is always equal and opposite, and either of this force is known as spring force.
For the same material,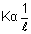 
. Where l is natural/relaxed length.
Spring force does not change instantly except when it is cut [So in all other cases it is a non impulsive force]
Illustration:
Find the acceleration (initial) of 1 and 2 if the upper spring is cut?
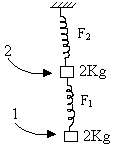
Fig (12)
When in equilibrium:
FBD of Body (2)
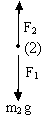
Fig (13)
F2 = F1 + m2g
FBD of Body (1)
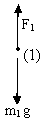
Fig (14)
F1 = m1g
So, F1 = 2g (N); F2 = 4g (N).
Now if upper one is cut then FBD looks like this:
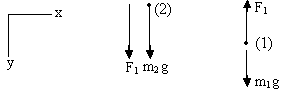
By the property of spring force F2 suddenly becomes zero while F1 remains unchanged.
So initially 
