Newtons Law of Motion - 3 (friction)

7) FRICTION:

Friction is the parallel component of contact force between two bodies in contact. When two bodies slip over each other the force of friction is called Kinetic friction, but when it has a tendency to slip and does not slip then the friction is static friction.

Block at Rest

Force applied but block does not move

Force applied to limiting value. Block just moves

Block starts moving

Friction=Force applied in opposite direction. Nature of friction being static.

Friction is still static and has maximum value at this point.  Friction = mSN. mS = coefficient of static friction.

Friction acts and has a constant value of mKN. mK= Coefficient of Kinetic friction. This is called Kinetic friction.

Friction = 0     

Graph:

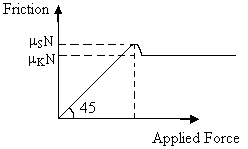
                        Fig (15)

Direction of Friction:

• Static friction is a self adjusting force. Its direction is not known till calculated.
• Kinetic friction’s direction is always opposite to the relative motion or relative velocity.

Dumb Question:

<!--[if !supportLists]--> 1)      Why is limiting friction more than kinetic friction?

Ans:

When two surfaces are in contact they look like this when magnified.

“To start a relative motion between these two surfaces requires a little more effort than to sustain that motion”

This statement directly gets translated to “The limiting friction is slightly more than the Kinetic friction”.

BELT FRICTION:

Pulley is locked, rope is light but friction exists between belt and pulley.

Then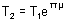

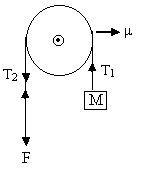
                                                      Fig (16)

Derivation:

               

            Fig (17)

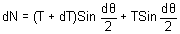               (Normal direction)

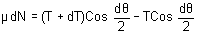           (Tangential direction)

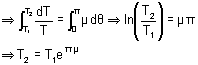
Illustration 1:

Example 4 Page 14 Narayana- Newton’s laws.

A block of mass M is at rest on a rough floor. The coefficient of static friction between block and the surface ism. A pulling force F is applied at angle q with the horizontal as shown.

a) For givenq, Find the minimum value of F needed to move the block.

b) If q is also adjustable, find the minimum value of F needed to move the block.

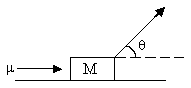
            Fig (18)

Solution:

a) FBD of block:

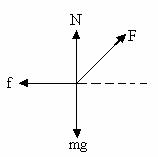
            Fig (19)

Break up of forces along with horizontal and vertical component.

 

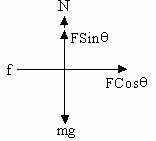
            Fig (20)

f_s £ LS₁F = mN

=  m (mg - FSinq)

For motion of block net horizontal force > 0

FCosq > m (mg - FSinq)

F (Cosq + mSinq) > m mg

b)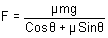

    

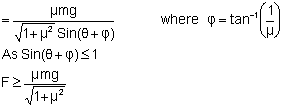
Thus the minimum force is required to move the block is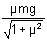

Dumb Question:

<!--[if !supportLists]--> 1)      How is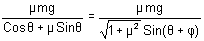

Ans:

Illustration 2:

Solved example HCV page 94.

Consider the situation in figure (21). The horizontal surface below the bigger block is smooth, the coefficient of friction between the blocks is m. Find the minimum and the maximum force F that can be applied in order to keep the smaller blocks at rest with respect to the bigger block.

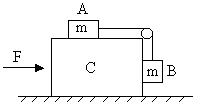
                    Fig (21)

Solution:

If no force is applied, the block A will slip on C towards right and the block B will move downward. Suppose the minimum force needed to prevent slipping is F, taking A+B+C as the system, the only external horizontal force on the system is F. Hence the acceleration of the system is

Now take the block A as the system. The force on A are

           

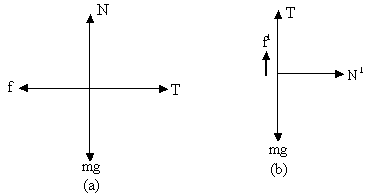
<!--[if !supportLists]--> 1)      Tension T by the string towards right

<!--[if !supportLists]--> 2)      Friction f by the block C towards left

<!--[if !supportLists]--> 3)      Weight mg downward and

<!--[if !supportLists]--> 4)      Normal force N upward.

For vertical equilibrium N = mg.

As the minimum force needed to prevent slipping is applied, the friction is limiting thus

f = mN = mmg

As the block moves towards right with an acceleration a,

T –f = ma

Or T - mmg = ma                                                               ----------------- (2)

Now take the block B as the system the forces are as shown in fig (b).      

<!--[if !supportLists]--> 1)      Tension T upward.

<!--[if !supportLists]--> 2)      Weight mg downward

<!--[if !supportLists]--> 3)      Normal force N¹ towards right

<!--[if !supportLists]--> 4)      Friction f¹ upward.

As the block moves towards right with an acceleration a, N¹ = ma.

As the friction is limiting, f¹= mN¹ = mma

For vertical equilibrium

T + f¹ = mg

Or T + mma = mg                                                           ------------------ (3)

Eliminating T from (1) and (3)

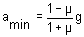
When a large force is applied the block A slips on C-towards left and the block B slips on C in the upward direction. The friction on A is towards right and that on B is downwards solving as above, the acceleration in this case is

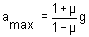
Thus a lies between 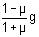 and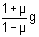

From (1) the force F should be between 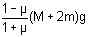and .