Nucleus - 5

(6) In an experiment on 2 radio active isotope of an elment which do not decay in to each other, mass ratio at a given instance was 3:1. That rapidly decaying isotope has larger mass & activity of 1 uc. intial the half life are known to be 12hrs and 16 hrs respectively . what would be activity of each isotope and mass ratio after 2 days.
Solution:- Assuming that mass ratio is same as ratio of no. of nucleii



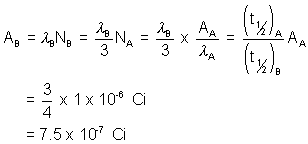
(7) It is found from an experiment that the radioactive substance one beta particle for each decay process.Also an average of 8.4 beta particles are emitted each second by 2.5 milligram of substance. The atomic weight of substance is 230
what is its half life?
Solution:- The activity = 8.4 sec^-1
Number of atoms in kilomole (i.e. 230kg) = 6.02 x 10²⁶,
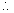N = x 2.5 x 10^-6 = 6.54 x 10^18>
    4 = N
       = x 6.54 x 10¹⁸


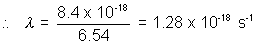
(8) radio Phosphrous-32 has half life of 14 days. a source containng this isotope has intial activity 10uc. (a) what is the activity of the source after 42 days?
(b) what time erpses before the activity of the source falls to 2.5 uci?
Solution:-
(a) The number of half-livesin 42 days 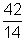= 3
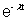A = A₀ = A₀ =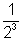

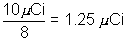
(b)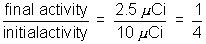
Time to decay to 1/4 of intial activity = 2 half lives
= 28 days

A radioactive source in the form of metal sphere of diameter 10^-3m emits particle at a constant rate of 6.25 x 10¹⁰ particles/s. If the source is electrically insulated, how long will take for its potential to rise by iv. assuming that 80% of the emitted particle escape from the source.
Solution:-
let after loosing ‘n’ electrons it acquire potential of (iv)

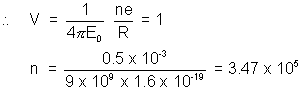
Actual no. of particles emitted = 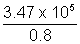= 4.378 x 10⁵
t x 6.25 x 10¹⁰ = 4.37 x 10⁵
t =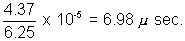

(10) What is the activity of one gram of 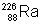, whose half-life is 1622 yrs?
Solution:- The number of atom 1g of radium is
N = 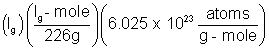= 2.666 x 10²¹
The decay constant is related to the half-life by

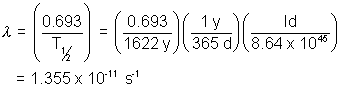
The activity is then found from
Activity = N =(1.355 x 10^-115^-1)(2.666 x 10²¹) = 3.612 x 10¹⁰dps
The definition of the curie is 1Ci = 3.7 x 10¹⁰. This is approx equal to the value above.

Medium:-

1. A nuclear reactor generates P = 20 mw power at efficiency 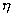= 60% by nuclear fission of aradio-nuclide whose half life is T = 2.2 yrs. if each fission releases energy E = 200 Mev, calculate time during which 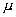= 10 mole of the redionuclide will be consumed completely.
   Solution:- To operate the nuclear reactor, let the number of fissions required per second be no, then energy released per second by fission reaction = n₀E
   Since, efficiency of the reactor is 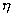, therefore , power output from the reactor = 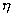n₀E
   But it is equal to P therefore P = 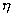n₀E or n₀ =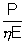
   let at an instant number of nuclei of radionuclide be n then rate of decay = n
   Where is decay constant which is equal to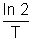
   hence, net rate of decrease of nuclei 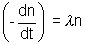n + n₀
   or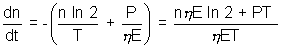
   
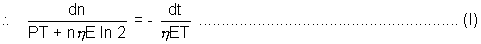
   at t = 0 number of nuclei are n = 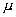N and time t is to be calculated when all the nuclei are consumed or when n = 0, t = ?
   Integrating equation (1) with these limits,