Parabola - 1
Introduction
Parabola is a curve of infinite extent and is not often obsened in real life as circles or shaight line are . However, the parabplaic curres are very important and have some vert good propertvies like the light raus reflected from parabolic surface passes through one foxed point. This property of parabola is luidely used in making lenses and in optics.
The brridges also take parabolic shape have been centuries lod. So, now let us start studying this interesting curre in more detail.
Parabola is locus of point which moves such that its distance from fixed point (focus) is always equat to its distance from fixed line (directrix) i.e. eccentricity, e = 1 .
Note: The distance from fixed point to the distance from fixed line is calle
General second degree equation: eccentncity.
The equation ax2 by + 2hxy + 2gx + 2fy + c = 0
(1) Second degrel thrms make a perfict square. or n 2 = ab.
Why ?
Let the fixed point be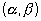
. and fixed line ax + by + 1 = 0 Let variable point be (h,k).
Now,according to the definition of parabola.
the distance of (h,K) from (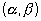) is same as distance from line ax + by + 1 = 0.
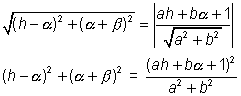
So locus of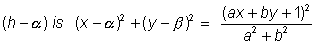
On simplification, we get
(a2 + b2)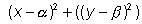
=(ax + by + 1)2
The expression reduces to
b2 x 2 + a2 y2 - 2abxy + .....linear terms .... + conjtant=(bx - ay)2 + ......linear terms + constant = 0.
So, second deqree terms make perfect squarc.
Dumb Question: Why is h2= ab same as second term making a perfect squarc ?
Ans The second degree terms in equation are
ax2 + by2+ 2hxy .
Now if h2 = ab
then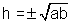
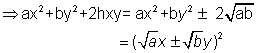
So, the two thing are same .
(2)
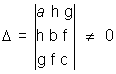
Illustration 1
Ide ntify the locus of point which move such that its distance from given point and line is equal ?
(i) (-3,7) is the point and x + 2y - 8 = 0 is given line .
Ans Now according to the question, let the point whose locus is to be determined be (x,y).
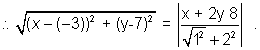
or,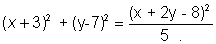
=>. 5 (x2 + 9 + bx + y2 + 49 -14y)
= x24y2 + 64 -16 x - 32y +4xy
= 4x2 + y2 - 4xy + 46x - 38y + 226 = 0
Considening 20 term, 4x2 y2 - 4xy = (2x - y)2 which is a perfect square.
Now consider
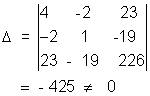
So, the locus is a parabola
(ii) (-6,7) is point and x + 2y - 8 = 0 is given line .
Ans. Note taht (- 6,7) satisfies the given line .
So, the locus is stratight line itself .
Standared Equation of parabola.
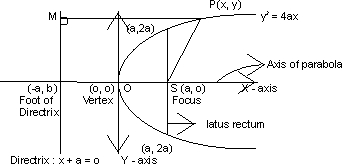
Important properties
(i) Vertex 0 (0,0)
(ii) Focus s(9,0)
(iii) Foot of directrix (-9,0)
(iv) Directrix x + a = 0
(v) Equation of catus rectum x = a
and length of Latus retum = 4a .
(vi) Axis y= 0.
(vii) Extremiofies of latus retum (91 2a) & (91-2a)
Note : Two parabolas are said to be equal if their length of latus rectii are equal .
The brridges also take parabolic shape have been centuries lod. So, now let us start studying this interesting curre in more detail.
Parabola is locus of point which moves such that its distance from fixed point (focus) is always equat to its distance from fixed line (directrix) i.e. eccentricity, e = 1 .
Note: The distance from fixed point to the distance from fixed line is calle
General second degree equation: eccentncity.
The equation ax2 by + 2hxy + 2gx + 2fy + c = 0
(1) Second degrel thrms make a perfict square. or n 2 = ab.
Why ?
Let the fixed point be
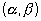. and fixed line ax + by + 1 = 0 Let variable point be (h,k).Now,according to the definition of parabola.
the distance of (h,K) from (
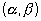) is same as distance from line ax + by + 1 = 0.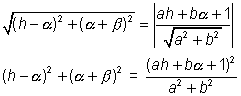So locus of
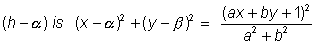
On simplification, we get
(a2 + b2)
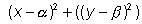=(ax + by + 1)2The expression reduces to
b2 x 2 + a2 y2 - 2abxy + .....linear terms .... + conjtant=(bx - ay)2 + ......linear terms + constant = 0.
So, second deqree terms make perfect squarc.
Dumb Question: Why is h2= ab same as second term making a perfect squarc ?
Ans The second degree terms in equation are
ax2 + by2+ 2hxy .
Now if h2 = ab
then
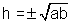
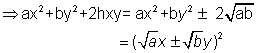
So, the two thing are same .
(2)
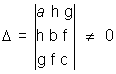
Illustration 1
Ide ntify the locus of point which move such that its distance from given point and line is equal ?
(i) (-3,7) is the point and x + 2y - 8 = 0 is given line .
Ans Now according to the question, let the point whose locus is to be determined be (x,y).
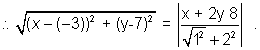
or,
=>. 5 (x2 + 9 + bx + y2 + 49 -14y)
= x24y2 + 64 -16 x - 32y +4xy
= 4x2 + y2 - 4xy + 46x - 38y + 226 = 0
Considening 20 term, 4x2 y2 - 4xy = (2x - y)2 which is a perfect square.
Now consider
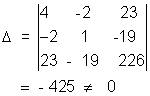
So, the locus is a parabola
(ii) (-6,7) is point and x + 2y - 8 = 0 is given line .
Ans. Note taht (- 6,7) satisfies the given line .
So, the locus is stratight line itself .
Standared Equation of parabola.
Important properties
(i) Vertex 0 (0,0)
(ii) Focus s(9,0)
(iii) Foot of directrix (-9,0)
(iv) Directrix x + a = 0
(v) Equation of catus rectum x = a
and length of Latus retum = 4a .
(vi) Axis y= 0.
(vii) Extremiofies of latus retum (91 2a) & (91-2a)
Note : Two parabolas are said to be equal if their length of latus rectii are equal .