Parabola - 2
Types of parabola
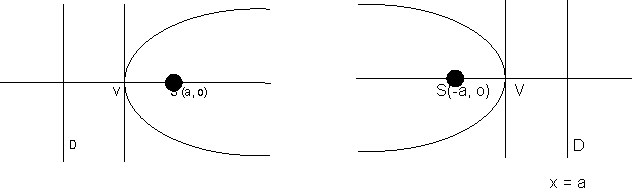
x + a = 0 y2 = 4ax, a > 0 Y2 = - 4ax, a > 0
s
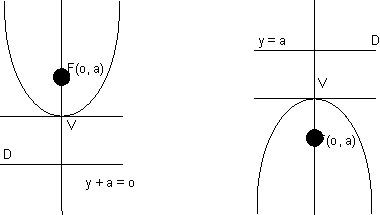
Transformation of parabola.
(a) (y - R)2 = 4a (x - h) , a > 0
The vcetex will be (h , k), openitng of parabola will be on = ve side of axis, axis will be || to x axis and dire ctrox well be || to y axis.
(b) (y - R2) = 4a (x-h), a < 0
Same as above except, the opening of parabolanwill be on -ve side of x - axis .
s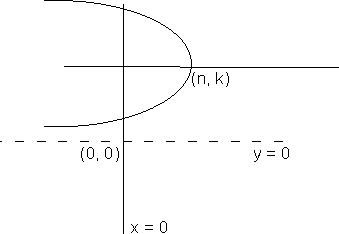
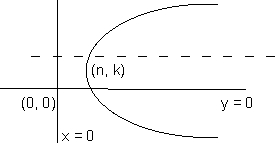
(c) (x -h 2) = 4a (y - yR), a > 0
The vertex will be at (h,K) opening of parabola will be on +ve side of yaxis , axis will be || t y - axid and directrix || to x - axis
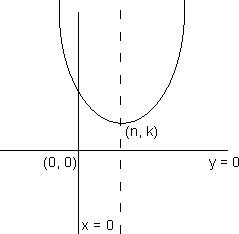
(d) (x -h 2) = 4a (y-K), a < 0
Same ad above except, lthe opening of parabola will be on -ve side of y-axis .
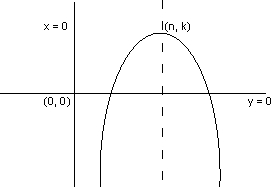
Illustration 2.
Find the vertex, axis, focus, and latus rectum of parabola
4y2+ 12x -x - 20y + 67 = 0
Ans The equation can be written as
y2- 5y = - 3x - 67/4 .
i.e. (y-5/22) = - 3x - 64/2 + 25/4 .
= - 3(x + 7/2)
So, this a transformed parabola whose vertex is (-7/2, 5/2), the axis is y = 5/2.
The length of latus rectum = |4a| = 3
and a = -3/4 .
So, focis is (-7/2 - 3/4 1 5/52)
= (-17/4 1 5/2).
Natations :
For standard parabola (y2 = 4ax)
1) S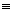
y2- 4ax
2) S1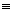y 12- 4ax1
3) Tyy1-2a(x + x1)
4) F(at ,2 2at)
Position of a point (x1,y1) w. r. t y2 = 4ax
If S1 > 0 => Outside parabola.
S1 < 0 => Inside parabola.
S1 0 => On parabola.
Why ?
Suppose a point is outside parabola .
s So, PL > PM.
=> PL 2 PM2
or y12 > y22
or y12 > 4ax1(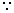
M lics oh parabola).
So, S1 > 0 => Point is outside parabola .
Similarily when point is inside the parabola .
S1 < 0 .
Dumb Question:- What dose inside and outside the parabola mean in a curre like parabola which is not closed ?
Ans :- the wird "outside" refers to the region from where tangent can be drawn . On other hand, the region from where tangent cannot be drawn is fefference as "in side" the parabola.
Par ame tric form.
x = at2, y = 2at where t is a parameter represents the parametric form.
(at2, 2at) is general point on parabola y2 = 4ax .
Illustration 2.
Find the equations of the parabola if the extremeties of its latus ractum are (3,5) and (3,7).
Ans.
Now the length of latus ractuin is
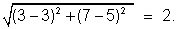
So, 4a = 2 or a = 1/2 .
Now middle point of catus ractum is
(3+3/2, 5+7/2) = (3,6) which is focus of parabola.
So the two cases as shown in figure below are possible.
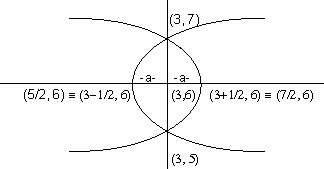
Since the vertex is at a distance a away from the parabola the vertices are (7/2, 6) and (5/2,6).
Now lBy transformation of parabolas the two parabolas possible are
(y-6)2 = 4(1/2) (x-5/2)
& (y-6)2 = 4(1/2) (x-7/2).
So, equation of parabolas are
(y-6)2 = 2 (x-5/2)
& (y-6)2 =2 (x-7/2)
x + a = 0 y2 = 4ax, a > 0 Y2 = - 4ax, a > 0
s
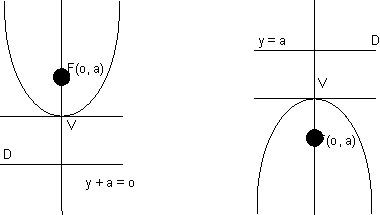
Transformation of parabola.
(a) (y - R)2 = 4a (x - h) , a > 0
The vcetex will be (h , k), openitng of parabola will be on = ve side of axis, axis will be || to x axis and dire ctrox well be || to y axis.
(b) (y - R2) = 4a (x-h), a < 0
Same as above except, the opening of parabolanwill be on -ve side of x - axis .
s
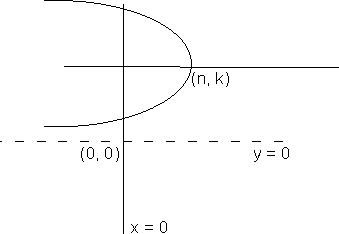
(c) (x -h 2) = 4a (y - yR), a > 0
The vertex will be at (h,K) opening of parabola will be on +ve side of yaxis , axis will be || t y - axid and directrix || to x - axis
(d) (x -h 2) = 4a (y-K), a < 0
Same ad above except, lthe opening of parabola will be on -ve side of y-axis .
Illustration 2.
Find the vertex, axis, focus, and latus rectum of parabola
4y2+ 12x -x - 20y + 67 = 0
Ans The equation can be written as
y2- 5y = - 3x - 67/4 .
i.e. (y-5/22) = - 3x - 64/2 + 25/4 .
= - 3(x + 7/2)
So, this a transformed parabola whose vertex is (-7/2, 5/2), the axis is y = 5/2.
The length of latus rectum = |4a| = 3
and a = -3/4 .
So, focis is (-7/2 - 3/4 1 5/52)
= (-17/4 1 5/2).
Natations :
For standard parabola (y2 = 4ax)
1) S
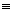y2- 4ax 2) S1
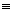y 12- 4ax13) T
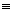yy1-2a(x + x1) 4) F
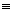(at ,2 2at)Position of a point (x1,y1) w. r. t y2 = 4ax
If S1 > 0 => Outside parabola.
S1 < 0 => Inside parabola.
S1 0 => On parabola.
Why ?
Suppose a point is outside parabola .
s So, PL > PM.
=> PL 2 PM2
or y12 > y22
or y12 > 4ax1(
M lics oh parabola).So, S1 > 0 => Point is outside parabola .
Similarily when point is inside the parabola .
S1 < 0 .
Dumb Question:- What dose inside and outside the parabola mean in a curre like parabola which is not closed ?
Ans :- the wird "outside" refers to the region from where tangent can be drawn . On other hand, the region from where tangent cannot be drawn is fefference as "in side" the parabola.
Par ame tric form.
x = at2, y = 2at where t is a parameter represents the parametric form.
(at2, 2at) is general point on parabola y2 = 4ax .
Illustration 2.
Find the equations of the parabola if the extremeties of its latus ractum are (3,5) and (3,7).
Ans.
Now the length of latus ractuin is
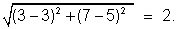
So, 4a = 2 or a = 1/2 .
Now middle point of catus ractum is
(3+3/2, 5+7/2) = (3,6) which is focus of parabola.
So the two cases as shown in figure below are possible.
Since the vertex is at a distance a away from the parabola the vertices are (7/2, 6) and (5/2,6).
Now lBy transformation of parabolas the two parabolas possible are
(y-6)2 = 4(1/2) (x-5/2)
& (y-6)2 = 4(1/2) (x-7/2).
So, equation of parabolas are
(y-6)2 = 2 (x-5/2)
& (y-6)2 =2 (x-7/2)