Parabola - 3
Dumb Question . Why two aprabolas are possible ?
Ans In this question only lasus ractum is given and two parabola are possible having same latus ractum on either side as shown in figure
Tangents to a parabola :
Let us find equation of tangents to parabola y2 = 4ax
(i)Equation of tangent of slope m : -
y = mx + a/m
And, the point of contact is p = (a/m2, 2a/m)
Why ?
Let line y = mx + c . be tangent to parabola y 2 = 4ax.
Saluing the two curres tom gether.
We get, (mx + c)2 = 4ax .
Since the line is tangent, this equation will have repeated roots.
So, D = O.
Now, (mx)2 + (2mc - 4a) x + c2 = 0
is equation.
D = 4 (mc-2a)2 - 4m2 c 2 = 0
=, (mc - 2a)2 - m2c2 = 0
=, (mc - 2a - mc)(mc - 2a + mc) = 0
=| - 4a (mc - a) = 0
=, c = a/m
(ii) Equation of tangent at (x1,y1)
yy1 = 2a (x+x1)
Why?
Now y2 = 4ax .
so, dy/dx = 2a/y
= is slope of tangent at (x1,y 1)
So,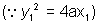
Put m - 2a / y1 in equation y = mx + a/m
=> y = 2a/y1 x + ay1/2a
=> yy1 = 2ax + 4ax1/2
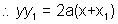
(iii) Equation of tangent at (at 2, 2at)
ty = x + at2
Why ?
Put x1 = at 2| y1 = 2at in
Equation yy1 = 2a (x + x1)
=> (2at) ly = 2a (x + at)2
= ty = x + at2
Illustation 4.
Prove that line x + my + am2 = 0 touches the parabola y 2 = 4ax. Also find or dinates of point of contact .
Ans:- Solving, parabola y2 = 4ax with line
x + my + am2 = 0, we get
y2 4a (-my - am2)
or. y 2 + 4amy + 4a2m2 = 0
or. (y + 2am)2 = 0 .
Since above is a perfect square, therefore both the values of y are equal. Hence given line is tangent to parabola and ordinates of the point to contact is - 2am (from y - 2am = 0)
Ptting, value of m in equation of the line we get x = am2.
Hence point of contact is (am2, - 2am)
Illustration 5
Find equation of straught lines touching both x2+ y2 = 2a2 and y2 = 8a
Ans:- the parabola is y2 = 8ax
or y2 = 4 (2a) x .
So, equation of tangent is
y = mx + 2a/m
or. m2x - lmy + 2a = 0
Since this is tan gent to x2 + y2 = 2a2, So the length of perpendicular from (0,0) must be equal to the radius ie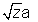
or
=> m4 + m2 - 2 = 0
=> (m2+2)(m2-1) = 0
=> m2-1 = 0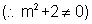
=>
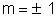
So, the equired tangent is
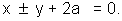
Equation of pair of tangents.
The equation of pair of tangent from (x1,y 1) is
t2 = ss1
or. (yy1- 2a(x + x1))2 = (y2 - 4ax)(y12 - 4ax1)
Why ?
Let p(x11 y1) be point from which tangents is drawin to y2 = 4ax
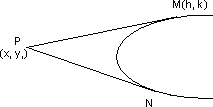
Let m(h1R) be any point on either of tangent of straight line joining p and M is
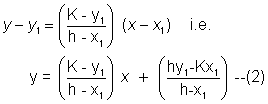
As this is tangent to given parabola, it should be of the form.
y = mx + a/m .-------(3)
Comparing (2) and (3) we get
Eliminating M from equation(4) and (5) we get .
=> a(h - x1)2 = (K-y1)(hy1- K x1)
Putting (x1y1) in place of (h1K) gibes equation of locus of M. as
a(x - x1)2 = (y - y1)(xy1 - yx1)
Which on rearranging gives .
Illustration 6.
Find the equation of tangents drawn to y2 + 12x = 0from point (3,8).
Ans Now, y2 = - 12x
or 4a = - 12
=> a = - 3
On . Comparing with standard form of tangent to parabola should be
y = mx + a/m or y = mx -3/m
Since tangent passes through (3,8) we ha
8 = 3m -3/m
or. 3mm2 - 8m -3 = 0
or (m - 3) (3m+1) = 0
=> m = 3, -1/3
Hence there L two tangents tnrough point (3,8)which are
3x - y -1 = 0
& x + 3y -27 = 0
Dumb Question Why tangent was taken in the form y = mx + a/m .?
Ans Whenever we have to take tangent from a point lying outside the parabola it is preferabee to take equation in this form as it is left second by satistying given opoint in the equation.
Normal to a parabola.
(1) Equation of normal at point (t)
y = -tx +2at +at3
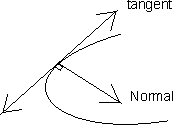
Why?
Slope of normal at (at2, 2at)
Equation of normal at (at2,2at) is y - 2at = - t (x-at2)
or y = - tx + 2at + at3
(2) Equation of normal slope m
Putting m = - t in above equation
y = mx - 2am - am3 (3) Equation of normal at (x1,y1)
y-y1= -y1/2a (x - x1)
Some important point .
(1) Maximum 3 normals can be drawn from anyn piont (h1K ) to parabola y2 = 4ax .
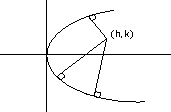
Why?
Equation of normal is
y = - tx + 2at + at3
So, 3 different value of t are possible when we put (h1 K) in given eqquation
i.r K = - t(n) + 2at + at3
Hence, 3different normals are possing .
(2) Three distirnt normals can be drawn from point (h1 K ) to parabola y24qx iff 4 > 2a .
Illustration 7.
Three normal to y2 = 4x pass through point (15,12) Show that one the normal is given by y =x - -3 and find equation of the others.
Ans:- y2 = 4x .
=> 4a =4 ie a = 1.
Any normal to parabola is
y = mx - 2am - am3
putting a= 1 , we get
y = mx - 2am - am3
As it passses through (15,12) we get
12 = 15m - 2m - m3
or m3 - 13m + 12 = 0
or (m - 1) (m + 4) (m - 3) = 0
m = 1, 3; - 4.
Hence three naormals are
y = x - 3
y = -4x + 72
y = 3x - 33.
Ans In this question only lasus ractum is given and two parabola are possible having same latus ractum on either side as shown in figure
Tangents to a parabola :
Let us find equation of tangents to parabola y2 = 4ax
(i)Equation of tangent of slope m : -
y = mx + a/m
And, the point of contact is p = (a/m2, 2a/m)
Why ?
Let line y = mx + c . be tangent to parabola y 2 = 4ax.
Saluing the two curres tom gether.
We get, (mx + c)2 = 4ax .
Since the line is tangent, this equation will have repeated roots.
So, D = O.
Now, (mx)2 + (2mc - 4a) x + c2 = 0
is equation.
D = 4 (mc-2a)2 - 4m2 c 2 = 0
=, (mc - 2a)2 - m2c2 = 0
=, (mc - 2a - mc)(mc - 2a + mc) = 0
=| - 4a (mc - a) = 0
=, c = a/m
(ii) Equation of tangent at (x1,y1)
yy1 = 2a (x+x1)
Why?
Now y2 = 4ax .
so, dy/dx = 2a/y
= is slope of tangent at (x1,y 1)So,
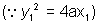
Put m - 2a / y1 in equation y = mx + a/m
=> y = 2a/y1 x + ay1/2a
=> yy1 = 2ax + 4ax1/2
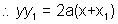
(iii) Equation of tangent at (at 2, 2at)
ty = x + at2
Why ?
Put x1 = at 2| y1 = 2at in
Equation yy1 = 2a (x + x1)
=> (2at) ly = 2a (x + at)2
= ty = x + at2
Illustation 4.
Prove that line x + my + am2 = 0 touches the parabola y 2 = 4ax. Also find or dinates of point of contact .
Ans:- Solving, parabola y2 = 4ax with line
x + my + am2 = 0, we get
y2 4a (-my - am2)
or. y 2 + 4amy + 4a2m2 = 0
or. (y + 2am)2 = 0 .
Since above is a perfect square, therefore both the values of y are equal. Hence given line is tangent to parabola and ordinates of the point to contact is - 2am (from y - 2am = 0)
Ptting, value of m in equation of the line we get x = am2.
Hence point of contact is (am2, - 2am)
Illustration 5
Find equation of straught lines touching both x2+ y2 = 2a2 and y2 = 8a
Ans:- the parabola is y2 = 8ax
or y2 = 4 (2a) x .
So, equation of tangent is
y = mx + 2a/m
or. m2x - lmy + 2a = 0
Since this is tan gent to x2 + y2 = 2a2, So the length of perpendicular from (0,0) must be equal to the radius ie
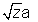
or
=> m4 + m2 - 2 = 0
=> (m2+2)(m2-1) = 0
=> m2-1 = 0
=>
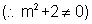
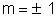
So, the equired tangent is
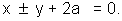
Equation of pair of tangents.
The equation of pair of tangent from (x1,y 1) is
t2 = ss1
or. (yy1- 2a(x + x1))2 = (y2 - 4ax)(y12 - 4ax1)
Why ?
Let p(x11 y1) be point from which tangents is drawin to y2 = 4ax
Let m(h1R) be any point on either of tangent of straight line joining p and M is
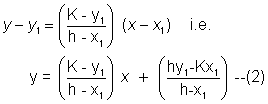
As this is tangent to given parabola, it should be of the form.
y = mx + a/m .-------(3)
Comparing (2) and (3) we get
Eliminating M from equation(4) and (5) we get .
=> a(h - x1)2 = (K-y1)(hy1- K x1)
Putting (x1y1) in place of (h1K) gibes equation of locus of M. as
a(x - x1)2 = (y - y1)(xy1 - yx1)
Which on rearranging gives .
Illustration 6.
Find the equation of tangents drawn to y2 + 12x = 0from point (3,8).
Ans Now, y2 = - 12x
or 4a = - 12
=> a = - 3
On . Comparing with standard form of tangent to parabola should be
y = mx + a/m or y = mx -3/m
Since tangent passes through (3,8) we ha
8 = 3m -3/m
or. 3mm2 - 8m -3 = 0
or (m - 3) (3m+1) = 0
=> m = 3, -1/3
Hence there L two tangents tnrough point (3,8)which are
3x - y -1 = 0
& x + 3y -27 = 0
Dumb Question Why tangent was taken in the form y = mx + a/m .?
Ans Whenever we have to take tangent from a point lying outside the parabola it is preferabee to take equation in this form as it is left second by satistying given opoint in the equation.
Normal to a parabola.
(1) Equation of normal at point (t)
y = -tx +2at +at3
Why?
Slope of normal at (at2, 2at)
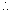Equation of normal at (at2,2at) is y - 2at = - t (x-at2) or y = - tx + 2at + at3
(2) Equation of normal slope m
Putting m = - t in above equation
y = mx - 2am - am3 (3) Equation of normal at (x1,y1)
y-y1= -y1/2a (x - x1)
Some important point .
(1) Maximum 3 normals can be drawn from anyn piont (h1K ) to parabola y2 = 4ax .
Why?
Equation of normal is
y = - tx + 2at + at3
So, 3 different value of t are possible when we put (h1 K) in given eqquation
i.r K = - t(n) + 2at + at3
Hence, 3different normals are possing .
(2) Three distirnt normals can be drawn from point (h1 K ) to parabola y24qx iff 4 > 2a .
Illustration 7.
Three normal to y2 = 4x pass through point (15,12) Show that one the normal is given by y =x - -3 and find equation of the others.
Ans:- y2 = 4x .
=> 4a =4 ie a = 1.
Any normal to parabola is
y = mx - 2am - am3
putting a= 1 , we get
y = mx - 2am - am3
As it passses through (15,12) we get
12 = 15m - 2m - m3
or m3 - 13m + 12 = 0
or (m - 1) (m + 4) (m - 3) = 0
m = 1, 3; - 4.Hence three naormals are
y = x - 3
y = -4x + 72
y = 3x - 33.