Parabola - 4

Dumb Question. How was m³ - 13m + 12 = 0
factorized into (m - 1) (m + 4)(m - 3) = 0. ?

Ans:- It was given in the question kthat it is to lbe shown that y = x - 3 is nirmal .
So, m = 1 should be factor of m³- 13m + 12 = 0 which it is.
Hence m³- 13 + 12 = 0 is written as
(m -1 ) (m² + m - 12 ) = 0
or (m -1) (m + 4) (m - 3) = 0
Chord of contact .



Equation of chord of contact: -
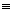
T 0
or yy₁ - 2a (x + x) = 0.

Why ?
Let point p(x₁, y₁) be
A (p₁q ) and B (h₁K ) on the parabola.
Equation of PB is lKy - 2a(x + h) = 0
Both these stangents pass through p(x + x₁)
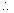
9y₁ = 2a (x₁ + p)
and Ky₁= 2a (x ₁ + h)
Now consiedr equation yy₁ - 2a (x + x₁ ) = 0
This equation is of first degree in x & y and it represcnts straight lline passing through
A (p₁q ) and B (h₁K )
Hence, equation yy₁- 2a (x + x₁) = 0
represents equation of line A B which is called chord of contact of point (x₁1y ₁)

Illustration 8.
From point (- 1, 2) tangent line are drawn to parabola y² = 4ax. find equation of hord of contact . Also find area of triangle formed by hoed of contac and the tangents.

Ans. Chord of lcontact of 0(-1,2) is
yy₁ = 2a (x + x₁)
or y = x - 1
Solving with parabola y = ² 4x we get the points




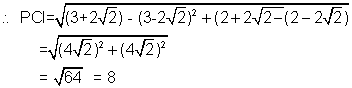
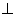
The distance of point 0(-1, 2)from line y = x -1 (Chord of contact) is


Chord of mid point ( x₁,y₁)




Note: Only one such chord is possible .

Why?
Any line through point (x₁, y₁) is
(y - y₁) = m(x - x₁ ----(1)
Now wehave to derermine value of m₁ its slope.
If it meets parabolain P( at₁, 2at₁ )and
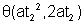
then its equation is
y(t₁ + t₂) - 2x - 2at₁t₂ = 0 ----(2)
So, by companing slopes in (1) and (2) we get
Since (x₁,y₁) is mid point of

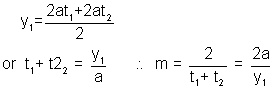
Putting
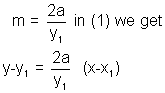
On reamanging, we get
yy₁ - 2a(x + x₁) = y₁² - 4ax₁
or

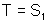Eauation of chord.

(i) Equation of chord joing (x₁),y₁) and (x₂, y₂) is
y(y₁ + y₂) = 4ax + y₁y₂

(ii)Equation of chard joing (at₁², 2at₂) and(at₁², 2at₂) is
y(t₁ + t₂) = 2 (x + at₁ t₂)

Note that both these results can be obtained by finding the middle point of the line joinign the two points and then using chord with mid point equation.

Illustration 9.
Show that locus of mid point of any focal chord is y² = 2ax - 2a²

Ans Let the mid point be (h₁K)
So, the equation of this kchord is
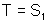
i.e yK - 2a (x+h) = K² - 4ah.
Now this chord is focal chord, si it must pass through (9,0).
=> (9,0) must satisty
yk -2a (x+h) = K² - 4aK
or . 0 - 2a(a + h) = k² - 4ah
or k² - 2ah + 2a² = 0
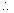
Locus is y²2ax + 2a² = 0
or y² = 2ax - 2a².

Diamcter
Thelocus of middle point of a system of || chords of a parabola is called a diamcter .
If y = mx + c represents a system of | | chord of parabola y² = 4ax, then likne y = 2a/m is equation of diamcter and this will meet parabola at
Why?
The chords y = mx + c where c varies infersed the parabola y² = 4ax at point y₁ and y₁
Now, y' and y" are roots of equation

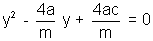
Which is obtained by solving y = mx + c
With y²= 4ax .
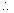
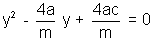
Equation is Let the middle point of the chords be (h,k)
So,
The equation of diametcr is y = 2a/m