Parabola - 5

Illustration 10.
The general equation to a system of parrallel chords in parabola is 4x - y + K = 0 . What is equation of corresponding diamcter ?

Ans Equation of parabola is y

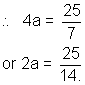
And the equation of system of | | chords
is 4x = y + K = y .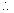
m = 4 .
So, diameetcr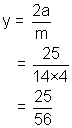
or 56y = 25.

Some Important and useful results

1. Focal distance of a point (at²,2at) is a + at²
   Why?
   
   
   
   Now focal distance = Pf = PB = a + at²
   = a +x,sub>1 (if (s₁, y₁) is point )
   
   
2. Foot of perperdicilar drawn from focus of parabola to any tangent will lie on tangent at vertex.
   Why?
   Equation of tangent is y = mx + a/m —(1)
   
   
   Equation of normal is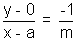
   or my + x = a —-(2)
   Solving (1) & (2) we get
   x = 0, y =a/m .
   (O,a/m) is the point and clearly it lies or y - axis
   
   
3. The circle descvibed on any focal chord as diamcter touches the directrix of the parabola .
   
   OR.
   
   Any two tangents drawn from point on the directrix to parabola are perpendicular to each other and the chord of contact is focal chord .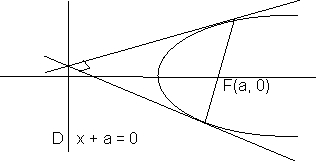
   
   
   4.) If any focal chord meets parabola at t₁and t₂.
   then t₁t₂ = - 1 .
   Why ?
   Slope of AC = slope of AB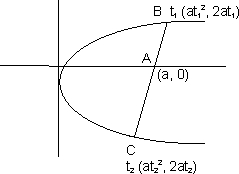
   
   
   So,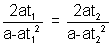
   =>t₁(1 - t₂²) = t₂(1 - t₁²)
   
   t₁- t₁t₂(t₂) = t₂ - t₁t₂ (t₁)
   
   (t₁ -t₂) + t₁t₂(t_{1- t2}) = 0
   
   (t₁ -t₂)( 1 + t₁t₂) = 0
   => t₁t₂ = - 1.
   
   Dumb Question Why t₁ - t₂ 0?
   
   Ans If t₁ -t₂ = 0 => t₁ = t₂
   So, this will mcan that point B and C are same point which is not true .
   Hence t₁ - t₂ 0
   
   5). If any chord joining t₁ and t₂ subtends right angle at vertex that t₁t₂ = - 4 .
   
   Why?
   Slope of VA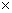 slope of VB = - 1 .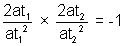
   
   t₁t₂ = - 4 .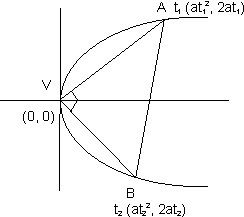
   
   
   
   6). Normal at t meets parabola at point (- t -2/t)
   Why ?
   Normal at t is ly = - tx + 2at + at³
   It meets parabola at t¹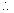
   t¹ will also satisfy the equation
   
   
   2ar¹ = - t (at'²) + 2at + at³
   
   or t(t'² - t²) + 2 ( t'-t) = 0
   
   or (t'-t) (t(t' + t) + 2) = 0
   
   => t' = t or t' = - t -2/t
   
   But t' t as lpoint is different . So, t' = - t-2/t
   
   

7. If two normals at point t₁ and t₂ meet again on parabola then t₁t₂ = 2 .
   Why ?
   Now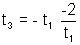 (from previous result) and also
   
   
   
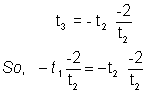
   => t₁t₂ = 2
   
   
8. Point of intersection of tangents at t₁ and t₂ is (at₁ t₂ ,a (t₁= t₂)).
   
   
   
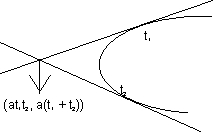
9. Point of intersection of normal drawn at t₁ and t₂ is
   [2a + a (t₁²+t₂² + t₁ t₂), - at₁t₂(t₁ + t₂)].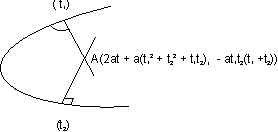
   
   
   
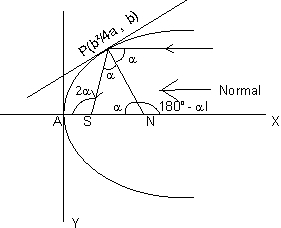
   (10) Reflection property of parabola. the tangent (pT) and normal (PN) ofparabola y²=4ax at p are the internal and external bisectors of SPM and Bp is to axis of parabola and BPN=SPN diagram 25
   
   
   
   Illustration:
   A ray of light coming along line y=b from the positive direction of x-axis strikes a concave mirror whose intersection with x-y plane is a parabola y²= 4ax. Find equation of reflected ray and show it passes through focus of parabola
   . both a and b are positive.
   Ans:- given parabola is y²=4ax.
   Equation of tangent at
   diagram26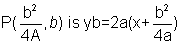
   slope of tangent=
   hence, slope of normal
   
   
   
   
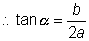
   slope of reflected ray
   =tan(180-2)
   =-tan 2
   
   =(y-b)(4a²-b²)=-(4ax-b²)b
   which clearly passes through focus s(a,0)
   
   Easy :-
   E_1 show that the line xcos +ysin=p
   touches the parabola y²
   =4ax if p cos+a sin²=0
   and that the point of contact is (atan² ,-2atan)
   
   Solution: The given line is
   xcos +ysin=p
   or y=-xcot+pcosec
   m=-cot and c=p cosec
   since the given line touches the parabola
   c=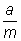
   or cm=a
   or(pcosec)(-cot=a
   and point of contact is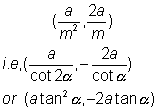
   
   
   E-2 show that normal to the parabola y₂=8x at the point(2,t) meets
   it again t (18,-12). find also the length of the normal chord.
   solution-
   
   
   
   s comparing the given parabola(i.e, y²=8x) with =4ax
   4a=8
   a=2
   since normal at (x1,y1) to the
   parabola y²=4ax is
   y-y1=
   Here x1=2 and y1=4
   equation of normal is,
   y-4=
   = y-4=-x+z
   =y+x-6=0…………(1)
   diagram solving (1) and y2 =8x
   y2=8(6-y)
   =y²+8y-48=0
   (y+12)(y-4)=0
   y=-12 and x=2
   hence point of intersection of normal and parabola are(18,-12) and(2,4) therefore
   normal meets the parabola at(18,-12)
   and length of normal chord is distance between their points