Parabola - 6
E-3 IF Three distinct and real normals can be drawn to y2=8x from the point (a,0) then show that a>4.
ans:- Equation of normal in terms of m is y=mx-4m-2m3=0
it passes through (a,0) then am-4m-2m3=0
m(a-4-2m2)=0
= m=0, m2=
for three distinct normal , (a-4)>0
=a>4
E-4 if y+b=m,(x+a) and y+b=m(x+a) are two tangents to the parabola y24ax, then show that m1m2=-1
which lies on the directrix x+a=0. hence th etwo tangents intersect on directrix which we know is the locus of perpendicular tangents .
hence m1.m2=-1
E-5 show that the parametric representation (2+t2,2t+1)
represents a parabola with vertex at (2,1).
Ans:- x=2+t2, y=2t+1.
Eliminating t= we get (y-1) 2 =4(x-2)
i.e, a parabola with vertex at (2,1).
Ans: Equation of the given parabola can be written as,
9x2+12x+4+18y-18=0
i.e, (3x+2)2=18(y-1)
Equation of tangent to the above parabola can be written as-
IF the tangent passes through (0,1) then we have,
0.m2 -4m-3=0
gives,m=-
hence equation of the required lines are,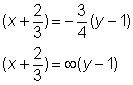
i.e, 12x+9y-1=0
and y-1=0
E-8: the tangents to the parabola y2 =4ax at p(at2,2at) and q(at22,2at2) intersect at r. prove that the area of the triangle
PQR is 
Ans: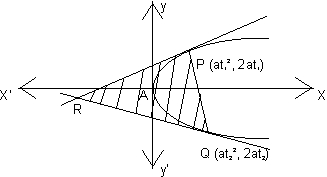
equation of tangents at p(at2,2at1) and Q(at22,2at2)
are, t1y=x+at12…………(1)
and t2y=x+at22
since point of intersection of (1) and (2) is r(at1t2) (at1t2,a(t1+t2)
E-6 the normals with slopes m1, m2, and m3 are drawn from apoint p not on the axis of the parabola y2
=4ax ifv m1 and m2=
results in the locus of p being a part of parabola, find the value of
Ans: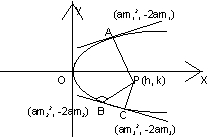
Any normal of the parabola y2=4x with slope m is
y=mz-2m-m3
thus, m1.m2.m3=-k
m3=-k(
m1m2=
= 
m3 is aroot of(1) then,
=k3+(2-h)k2-k3=0
locus of p(h,k) is,
y3+(2-x)y2-y3=0
(p does not lie on the axis of the parabola)
=y2=2x-22+3
it is a part of the parabola y2=4x
then 2=4
and -22+3=0
=-2=0
=2
E-7: find the equation of aline which touches the parabola
9x2+12x+18y-14=0
and passes through the point (0,1).
AREA OF TRAINGLE: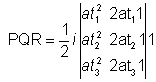 
.
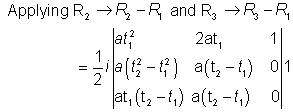
Expanding with respect to first row-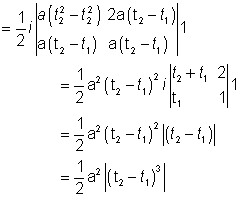
.
E-9: Find the length of the normal chord to the parabola y2=4x which substends a right angle
at the vertex Ans:- a=1 for parabola PQ being normal chord.
PQ substend a right angle at vertex,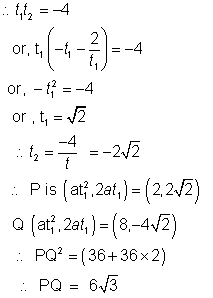
E - 10. An equilateral triangle SAB is inscribed in the parabola y2 = 4ax Having its focus at ‘S’.
It chord AB lies towards the left of S. Then find the side length of this triangle.
Ans: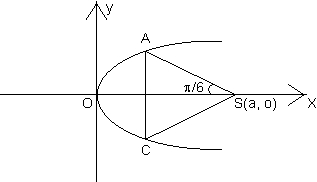
let A=(at12,2at1),B=(at22-2at1)
we have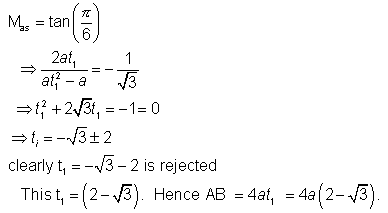
Q��� Prove that 9x2 - 24xy + 16y2 - 20x - 15 y -
60 = 0 represents a parabola. Also find its focus and directrix.
Ans: Here h2-ab=(-12)2-9x16=144-144=0 also 
the equation represents a parabola Now, the equation is(3x-4y)2=5(4x+3y+12) clearly
, the lines 3x-4y=0 and 4x+3y+12=0 are perpendicular to each other.so, let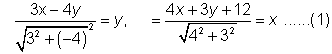 
the equation of the parabola becomes -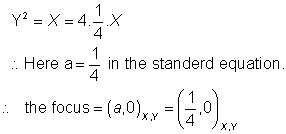
Now if 
then we havefrom the equations of tranformation in(1)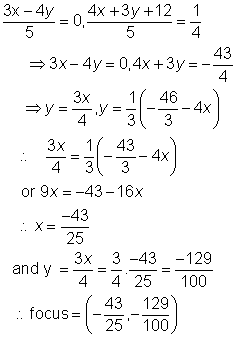
The equation of directrix is,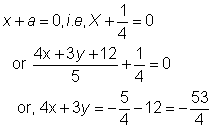
The directrix is 