Parabola - 7
Dump Question: The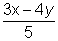 was written as Y and
was written as Y and 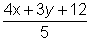 was
was
written as y.how?
Ans: The lines 3x-4y=0 and 4x+3y+12=0 are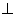 to each other as clear from
to each other as clear from
their slopes. so, the rotation of axis and transformation of axes was performed
to get the desired easy form of parabola.
Q.2:- Three normals from a point to the parabola y2 = 4ax meet the axis of the parabola in points whose abscissa
are in A.P. Find the locus of the point. Ans : The equation of any normal to
the parabola is Y = mx - 2am -am3 It passes through the point (h,k) if am3
+ m (2a - h) + k = 0 ??????. (1) the normal cuts the axis of the parabola viz
, y = 0 at point where x = 2a + am2 hence the abscissa of the point in which
the normal through (h,k) meet the axis of the parabola are. X1 = 2a + am12 , x2 = 2a + am23 , x3 = 2a + am3 2 Since X1 ,x2, x3 are in A.P. (2a + am21) +( 2a + am23) = 2 (2a + am22)
= m12+m22=2m22..........(2)
also from (1) m1+m2+m3=0..............(3)
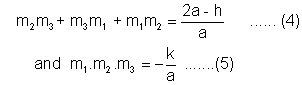
from (3) (m1+m2)2=m22==m12+m32+2m1m3=m22
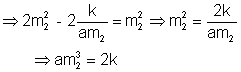
Since m2 is a root of (1), am2 3+m2(2a-h)+k=0
= 2 k+m 2 (2a-h) + k = 0
27 ak2 = 2 (h - 2a)3
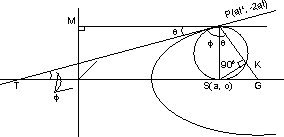
Hence the locus of(h,k) is 27ay2=2(x-2a)3 M-3- prove that the length of the intercept on the normal at the point p(at2,2at) of a parabola
y2=4ax made by the circle on the line joining the focus and point p as diameter is a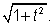
ANS: let the normal at p(at2,2at) cut the circle in k and the axis of parabola at g then pk is required intercept.
SP=PM=a+at2
Since angle in a semicircle being right angle . SPR=90.
SPR=90.
and normal at p(at2,2at) is
y = - tx+2at+at3
= tx + y - 2at - at3=0
 SK is the perpendicular distance from s(a,0) to the normal(1)
SK is the perpendicular distance from s(a,0) to the normal(1)
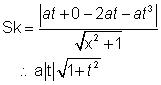
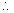 in
in  SPK
SPK
(PK)2 = (SP)2 - (SK)2
= a2(1+t2)2 - a2t2 (1 + t2)
= a2 (1+t2)
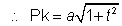
Dumb Question:- why is SP=PM in the above question? Ans: the point p lies on the parabola . so the distance of p from directrix is same as the distance from the focus. and hence SP=PM. Q-4:- Three normals are drawn from the point (0,0) to the currve y2=x. show that c must be greater than 1/2. one normal is always the x-axis . Find c for which the other two normals are perpendicular to each other.
Ans: Equation to normal to the parabola
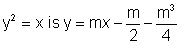 is passing through (c,o)
is passing through (c,o)
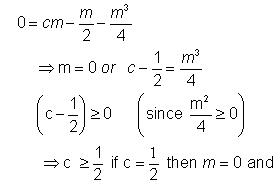
Then only one normal will be there i.e , x axis
Now the slope of other two normal are
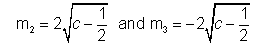
For these normals to be to each other
to each other
we need m2.m3=-1
so,
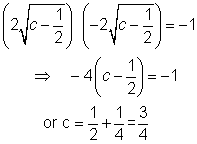
M-3:- Find the equation to the common tangents to the circle x2+y2=2a2
and the parabola y2=8ax.
Ans :-
The Equation of any tangent to the parabola y2=8ax i.e,
will touch the circle x2+y2=2a2 if
radius =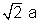
= length of the perpendicular from the centre(0,0) to the line
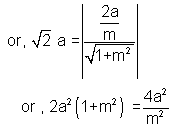
or, m2(1+m2)=2
or, m4+m2-2=0
or,(m2+2)(m2-1)=0
But m2+2=0 gives non real values of m.
 m2-1=0;
m2-1=0;
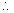 m=
m=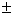
Putting m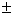 in (1) we get the equation of common tangents are
in (1) we get the equation of common tangents are
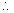 the equations of common tangents are.
the equations of common tangents are.
y =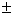 x
x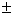 2a
2a
or y=x + 2a and y=-(x+2a)
Dumb question : why y=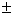 x
x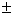 2a gave only four equations of straight line
2a gave only four equations of straight line
y=x+2a & y= -(x+2a) where as four lines are possible?
Ans:- Note that the equation of tangent in y=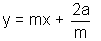
So, it is not possible m with x be +ve and m with 2a be -ve . hence y=x-2a & y=-x+2a are impossible solutions.
Q.7: Prove that the circle circumscribing the triangle formed by tangents to a parabola passes through the focus
Ans: Let P(at12, 2at1),q(at22,2at2) and r(at32,2at3) be three points on the parabola y2=4ax
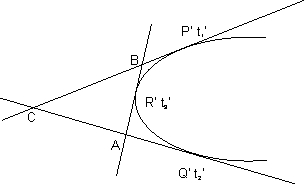
The equation of tangents at P't11 and Q't2' are
Y t11 = x + at12
Y t2 = x + at22
Solving these, x = at1t22 and y = a(t1 + t2 )
The point of intersection C of the tangents at P and Q is
{ at1 t2 , a(t1 + t2 )}.
similarly other points of intersection of tangents are
B = {at3t1, a(t3+t1)},A={at2t3,a(t2+t3)}
let the equation of circumcircle of the ABC be
ABC be
x2+y2+2gx+2fy+c=0------------(1)
(1) will pass through the focus (a,0) if
a2 + 2ga + c=0..........................(2)
A,B,C are points on (1) .so-
a2 t12 t22 +a2 (t1+t2)2+ 2g.at1t2+2.f.a(t1+t2)+c=0.........(3)
a2 t22 t32 +a2 (t2+t3)2+ 2g.at2t3+ 2.f.a(t2+t3)+c=0...........(4)
a2 t32 t12 +a2 (t3+t1)2+ 2g.at3t1+ 2.f.a(t3+t1)+c=0...........(5)
(3)-(4)
a2 t22( t12-t 32+a2 (t1-t3)(t1+2t2 +t3+2g.at2(t1- t3)+2.f.a(t1-t1)+c=0
or, a2 t22 (t1+t3+a2(t1+2t2 +t32g.at2t2+ 2.f.a=0..........(6)
similarly (4)-(5)
=> a2[t22 (t1 + t3) - 32(t2 + t1) + t2 - t3] + 2g.a(t2 - t3) = 0
or,a [t2t3(t2 - t3) + t1(t22 - t32) + t2-t3)] + 2g(t2-t3) = 0
or,a[t2t3 + (t1t2) + t1t3 + 1] + 2g=0
 2g=-a(1 + t1t2 + (t2t3) + t3t1)
2g=-a(1 + t1t2 + (t2t3) + t3t1)
From t3x(6) - t2 X(7),we get
2f=-a(t1 + t2 + t3-t1t2t3)
putting values of 2g, 2f in (3) we get
 the equation of the circumcircle is-
the equation of the circumcircle is-
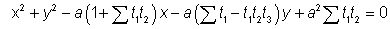 -
-
it passes through(a,0) because.-
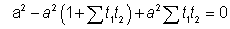 -
-
Hence the problem.-
written as y.how?
Ans: The lines 3x-4y=0 and 4x+3y+12=0 are
their slopes. so, the rotation of axis and transformation of axes was performed
to get the desired easy form of parabola.
Q.2:- Three normals from a point to the parabola y2 = 4ax meet the axis of the parabola in points whose abscissa
are in A.P. Find the locus of the point. Ans : The equation of any normal to
the parabola is Y = mx - 2am -am3 It passes through the point (h,k) if am3
+ m (2a - h) + k = 0 ??????. (1) the normal cuts the axis of the parabola viz
, y = 0 at point where x = 2a + am2 hence the abscissa of the point in which
the normal through (h,k) meet the axis of the parabola are. X1 = 2a + am12 , x2 = 2a + am23 , x3 = 2a + am3 2 Since X1 ,x2, x3 are in A.P. (2a + am21) +( 2a + am23) = 2 (2a + am22)
= m12+m22=2m22..........(2)
also from (1) m1+m2+m3=0..............(3)
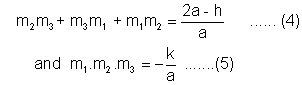
from (3) (m1+m2)2=m22==m12+m32+2m1m3=m22
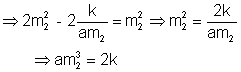
Since m2 is a root of (1), am2 3+m2(2a-h)+k=0
= 2 k+m 2 (2a-h) + k = 0
27 ak2 = 2 (h - 2a)3
Hence the locus of(h,k) is 27ay2=2(x-2a)3 M-3- prove that the length of the intercept on the normal at the point p(at2,2at) of a parabola
y2=4ax made by the circle on the line joining the focus and point p as diameter is a
ANS: let the normal at p(at2,2at) cut the circle in k and the axis of parabola at g then pk is required intercept.
SP=PM=a+at2
Since angle in a semicircle being right angle .
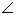 SPR=90.
SPR=90.and normal at p(at2,2at) is
y = - tx+2at+at3
= tx + y - 2at - at3=0
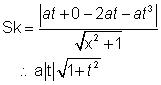
(PK)2 = (SP)2 - (SK)2
= a2(1+t2)2 - a2t2 (1 + t2)
= a2 (1+t2)
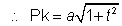
Dumb Question:- why is SP=PM in the above question? Ans: the point p lies on the parabola . so the distance of p from directrix is same as the distance from the focus. and hence SP=PM. Q-4:- Three normals are drawn from the point (0,0) to the currve y2=x. show that c must be greater than 1/2. one normal is always the x-axis . Find c for which the other two normals are perpendicular to each other.
Ans: Equation to normal to the parabola
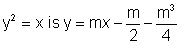 is passing through (c,o)
is passing through (c,o)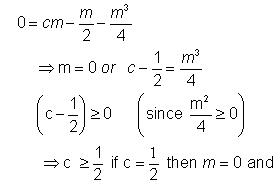
Then only one normal will be there i.e , x axis
Now the slope of other two normal are
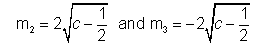
For these normals to be
 to each other
to each otherwe need m2.m3=-1
so,
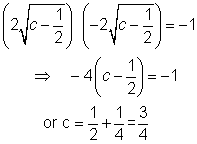
M-3:- Find the equation to the common tangents to the circle x2+y2=2a2
and the parabola y2=8ax.
Ans :-

The Equation of any tangent to the parabola y2=8ax i.e,
will touch the circle x2+y2=2a2 if
radius =
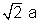
= length of the perpendicular from the centre(0,0) to the line
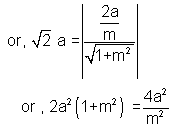
or, m2(1+m2)=2
or, m4+m2-2=0
or,(m2+2)(m2-1)=0
But m2+2=0 gives non real values of m.
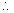 m2-1=0;
m2-1=0; m=
m=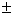
Putting m
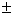 in (1) we get the equation of common tangents are
in (1) we get the equation of common tangents are the equations of common tangents are.
the equations of common tangents are.y =
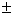 x
x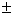 2a
2aor y=x + 2a and y=-(x+2a)
Dumb question : why y=
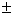 x
x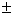 2a gave only four equations of straight line
2a gave only four equations of straight liney=x+2a & y= -(x+2a) where as four lines are possible?
Ans:- Note that the equation of tangent in y=
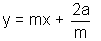
So, it is not possible m with x be +ve and m with 2a be -ve . hence y=x-2a & y=-x+2a are impossible solutions.
Q.7: Prove that the circle circumscribing the triangle formed by tangents to a parabola passes through the focus
Ans: Let P(at12, 2at1),q(at22,2at2) and r(at32,2at3) be three points on the parabola y2=4ax

The equation of tangents at P't11 and Q't2' are
Y t11 = x + at12
Y t2 = x + at22
Solving these, x = at1t22 and y = a(t1 + t2 )
The point of intersection C of the tangents at P and Q is
{ at1 t2 , a(t1 + t2 )}.
similarly other points of intersection of tangents are
B = {at3t1, a(t3+t1)},A={at2t3,a(t2+t3)}
let the equation of circumcircle of the
 ABC be
ABC bex2+y2+2gx+2fy+c=0------------(1)
(1) will pass through the focus (a,0) if
a2 + 2ga + c=0..........................(2)
A,B,C are points on (1) .so-
a2 t12 t22 +a2 (t1+t2)2+ 2g.at1t2+2.f.a(t1+t2)+c=0.........(3)
a2 t22 t32 +a2 (t2+t3)2+ 2g.at2t3+ 2.f.a(t2+t3)+c=0...........(4)
a2 t32 t12 +a2 (t3+t1)2+ 2g.at3t1+ 2.f.a(t3+t1)+c=0...........(5)
(3)-(4)
a2 t22( t12-t 32+a2 (t1-t3)(t1+2t2 +t3+2g.at2(t1- t3)+2.f.a(t1-t1)+c=0
or, a2 t22 (t1+t3+a2(t1+2t2 +t32g.at2t2+ 2.f.a=0..........(6)
similarly (4)-(5)
=> a2[t22 (t1 + t3) - 32(t2 + t1) + t2 - t3] + 2g.a(t2 - t3) = 0
or,a [t2t3(t2 - t3) + t1(t22 - t32) + t2-t3)] + 2g(t2-t3) = 0
or,a[t2t3 + (t1t2) + t1t3 + 1] + 2g=0
 2g=-a(1 + t1t2 + (t2t3) + t3t1)
2g=-a(1 + t1t2 + (t2t3) + t3t1)From t3x(6) - t2 X(7),we get
2f=-a(t1 + t2 + t3-t1t2t3)
putting values of 2g, 2f in (3) we get
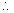 the equation of the circumcircle is-
the equation of the circumcircle is- -
-it passes through(a,0) because.-
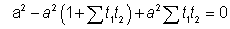 -
-Hence the problem.-