Dumb Question: How does the fact that the circle x
2+y
2+2gx+2fy+c=0 passes through(a,0) leads to the condition -
a
2+2ga+c=0-
Ans:- Since the circle passes through (a,0) the equation of circle must satisfy the point(a,0)-
so, a
2+0
2+2g(a)+2f(0)+c=0-
0r a
2+2ga+c=0 is obtained.-
let c1 and c2 be respectively the parabola x
2=y-1 and y
2=x p be any point on c1 and q be any point on c2. Let p1 and Q1 be reflections of P and Q-
respectively with respect to the line=y
prove that p1 lies on c2, Q1 lies on c1 and PQ> min[pp1,QQ1]-
Hence or otherwise determine points p
0 and Q
0 on the parabolas c1 and c2 respectively. such that p
0Q
0 (Pq)-for all pairs of points (p,Q) with p on c1 and Q on c2.-
Ans:
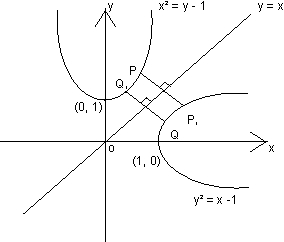
Let co-ordinates of p and q are p(t, t
2+1) and Q (s
2 + 1, s) which lies on x
2=y-1
and y
2=x-1 respectively.-
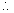
p1 and Q1 be reflections of P and Q respectively with respect to the line y=x then-
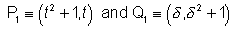
we have, (PQ
1)
2=(t-s)
2+(t
2-s
2)
2(p
1Q)
2=>PQ1=PIQ
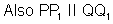
Thus PP1QQ1 is an isosceles trapezium
we have Pq> min {PP1,QQ1}
Let us take min {PP1,QQ1}=PP
1then (PQ)
2=(pp
1)
2=>(t
2+1-t)
2+(t-t
2-1)
2=2(t
2-t+1)
2=f(t)say
we have f'(t)=4(t
2-t+1)(2t-1)
NOw
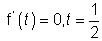
Also
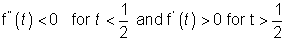
Hence f(t) is least when t=1/2 point p
0 on c1 is
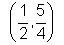
and p1(which we take as Q
0and c2 are
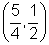
.Note that PQ
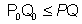
for all pairs of(P,Q) with p on C1 and Q on c2.
Hence proved.
Dumb Question:- f' (t) is4(t
2-t+1)(2t-1), but the only solution is t=1/2. what about the factor t
2-t+1?
Ans:- Note that t
2-t+1=
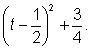
Now, this a positive quantity if t is + ve.
The coordinate plane is a real plane Where the points can take only real values and hence t has to real only. So, t2 - t + 1 cannot be zero.
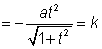
=k (from the equation)
from (1) the equation of the axis of the parabola in x,y coordinate becomes-
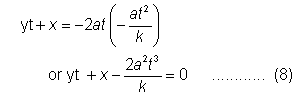
The given parabola is x
2=-8k(y-2k)........(9)
solving (8) and (9) we get
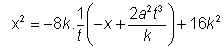
here D= 64k
2-64t
2(a
2t
2-k
2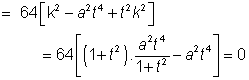
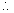
the axis given by(8) touches the given parabola.
Note:- if we take
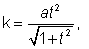
, the points of intersection of the axis and the given parabola will be imaginary.
Que:- A parabola drawn touching the axis of x at the origin and having its vertex at a given distance k from the x - axis . Prove that
the axis of parabola is a tangent to the parabola x2 + 8k(y - 2k) = 0.
Ans : Let the equation of the parabola be Y2 = 4ax

Any tangent to it at the point (at
2, 2at) is
Yt = X +at
2.........(1) The normal at the point( at
2, 2at) is
Y + tX = 2at + at
3........(2)
Take the equations of transformation -

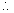
in xy coordinates p=(0,0) and PT is the axis which is
tangent to the parabola at the origin.
Now,

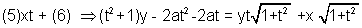
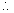
the axis of the parabola(y=0) becomes-
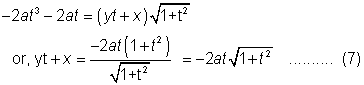
the distance of the vertex v(0,0) in the x,y coordinates from pt -
keywords:-
1. Parabola
2. focus
3. Directrix
4. Eccentricity
5. Vertex
6. Axis.
7. Latus rectum.
8. Diameter
9. Focal distance
10. Focal Chord.