Dispute in 1654 led to the creation of a mathematical theory of prabability by two famous french mathematicians Blaise Pascal and Pierrede Fermet . First fundamental principles of prabobility theory were formulated for Ist time In popular dice game. Consisted in throwing a pair of dice 24 time, the problem was to decide whether or not to bet even money on occurrence of at least one "double six" during 24 throws. By gambling rule chevalier de mere believed it would be profitable but c caluclation shows just opposite .
Dutch scientist christion Huygens in 1657 published the first book of probability entitled De Ratiociniis in Ludo Aleac.
In 1812 pierse de laplace introduced a host of new ideas and mathematical techniques in his p book .
Equally likely - If two events are called equally likely if none of the events have preference of occurence of other .
Nutually exclusive :- If occurence of one event rules out lthe ocurrence of other .
Exhaustive :- Set of event in experiment is said to exhaustive it nothing happen than those listed possible out comes can occur as a consequence of the experiment .
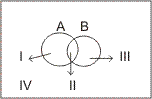
Total out comes of experiment is called sample space .
A; 'm' out comes favour the occurence of event A .
P (A) =
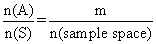
P(
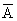
) = complement of A P (A
c)
P (
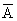
)=
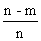
= 1 - P (A)
P(A) + P(
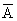
) = 1
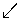
0
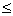
P (A)
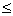
1
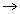
sure ivent
Impossible event img sure event
Example of kequally likely events :-
When a unbiased coin is tossed then occrenice of head or tail are equally likely .
Example of mutually exclusive event -
Let sample space of unbised die is die is S = {1, 2, 3, 4, 5, 6} in which E
1 = {1, 2, 3,} = ecent of occurrence lof no. less than 4 & E
2 = {5, 6} = event of occurrence of no. greater than 4.
cleaarly . E
1 
E
2 =
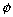
so, E
1 and E
2 are mutually exclusive .
Examples of exhaustiv event :-
Let sample space of unbiased die is S = {1, 2, 3, 4,5, 6} in which E
1 = { 1, 2, 3, 4} = Event of occurence of no . less tahn 5.
& E
2 = {3, 4, 5, 6} = Event of occurence of no. Greater than 2.
Then E
1U E
2 = {1, 2, 3, 4, 5, 6} = 5
Hence E
1 & E
2 are exhaustive events .
Odds in favour :- If 'a' is no of cases favourable to odds in favour of E are a : b & odds against of E are b : a.
P (E) =
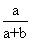
& P (E
1) =
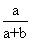
P(E) + P(E
1) = 1
Illustration :- A person while dialing 7 digit phone no. forget last two digit and he randonly dials 2 numbers .
Find the chance of currect no.
Ans - There are 10 digit on phone.
1
st digit can be dialled in 10 ways.
2
n digit can be dialled in 10 way .
sample space (total no. of ways two digit can be dialled)
= 10 X 10 = 100
But there is only 1 currect no.
So, P (A) = 1/100
Independent and dependedt event :- Two event are said to be independent if occurence or non - occurence of are does affects the probabitity of occurence or non-occurence of the other .
eg. Occurence of head or tail is independent on each other.