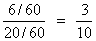Probability - 3
Bagrang's relation ship
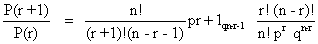
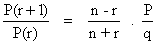
Dumb Question :- How relation P (getting r' s success)
= Pr qn-r nC r
Ans - In this P is probability of getting success and q is probability of getting failure and p + q = 1
Sclection of r success out of n out comes = nCr
img..... P(getting r' s success)
= P x P x P...............r times x q x q x.............(n - r) times x nCr
Illustration :- A die is rolled n times. Find the value of n if probability of getting at least one ace is 91/216
Ans P(getting at least one ace) = 1 - P(no ace)
P(1) = 1/6 P(not 1) = 5/6
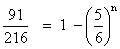
=> n = 3
Probability theorem - (Baye's theorem)
If an event A can occur with n mutually exclusive, exhaustive
event B1, B2, ..............Bn and probability of P(A/B1),
P(A/B2), ................P(A/Bn) is known. Then probability .
P(Bi/A) =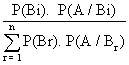
P(A img Bi) = P(Bi). P(A/Bi)
= P (A). P(Bi/A)

P(A) = P(A img B1) + P(A img B2) + ......+ P(Bn) P(A/Bn)
=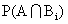 P(Bi) P(A / Bi)
P(Bi) P(A / Bi)
=P(A). P(Bi / A)
P(A) =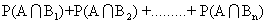
=P(B1) P(A / B1) P (A / B2) + ............+ P(Bn) P(A / Bn)
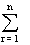 P(Br) P (A / Br)
P(Br) P (A / Br)
Illustration :- A bag cintains 5 balls of unknown color. Two balls are drqwn and both are found to be white. Find the chance that there are 4 white ball in box . Assume any no. of white ball equally likely .
Ans - A : Two balls drawn from a bag contuins 5 balls.
both are white
B0 : 0 white ball
B1 : 1 white ball
B2 : 2 white ball
B3 : 3 white ball
B4 : 4 white ball
B5 : 5 white ball
P(B0) = P(B0) = P(B1) = P(B3) = P(B4) =P(B5) =P(B6) = 1/6
P(A/B0) = 0 P(A/B1) = 0
P(A/B2) =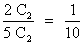
P(A/B3) =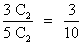
P(A/B4) =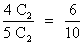
P(A/B5) =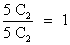
P(B4/A) =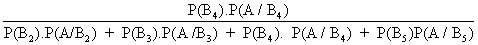
=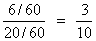
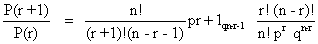
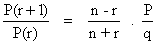
Dumb Question :- How relation P (getting r' s success)
= Pr qn-r nC r
Ans - In this P is probability of getting success and q is probability of getting failure and p + q = 1
Sclection of r success out of n out comes = nCr
img..... P(getting r' s success)
= P x P x P...............r times x q x q x.............(n - r) times x nCr
Illustration :- A die is rolled n times. Find the value of n if probability of getting at least one ace is 91/216
Ans P(getting at least one ace) = 1 - P(no ace)
P(1) = 1/6 P(not 1) = 5/6
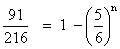
=> n = 3
Probability theorem - (Baye's theorem)
If an event A can occur with n mutually exclusive, exhaustive
event B1, B2, ..............Bn and probability of P(A/B1),
P(A/B2), ................P(A/Bn) is known. Then probability .
P(Bi/A) =
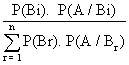
P(A img Bi) = P(Bi). P(A/Bi)
= P (A). P(Bi/A)

P(A) = P(A img B1) + P(A img B2) + ......+ P(Bn) P(A/Bn)
=
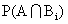 P(Bi) P(A / Bi)
P(Bi) P(A / Bi)=P(A). P(Bi / A)
P(A) =
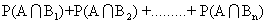
=P(B1) P(A / B1) P (A / B2) + ............+ P(Bn) P(A / Bn)
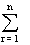 P(Br) P (A / Br)
P(Br) P (A / Br)Illustration :- A bag cintains 5 balls of unknown color. Two balls are drqwn and both are found to be white. Find the chance that there are 4 white ball in box . Assume any no. of white ball equally likely .
Ans - A : Two balls drawn from a bag contuins 5 balls.
both are white
B0 : 0 white ball
B1 : 1 white ball
B2 : 2 white ball
B3 : 3 white ball
B4 : 4 white ball
B5 : 5 white ball
P(B0) = P(B0) = P(B1) = P(B3) = P(B4) =P(B5) =P(B6) = 1/6
P(A/B0) = 0 P(A/B1) = 0
P(A/B2) =
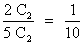
P(A/B3) =
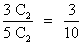
P(A/B4) =
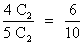
P(A/B5) =
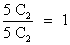
P(B4/A) =
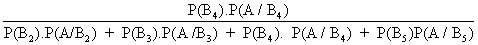
=