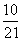Probability - 6
Medium level
Q. 1- A, B and C are three event such that -
P(exatly one A or B) = P(exactly one B C)
=> P(exactly one C or A) = P
and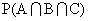 = p2 and A, B and C are
= p2 and A, B and C are
exhaustive. Find = value of P .
Ans - Not :- In exhaustive events
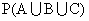 = 1
= 1
P = P (a) + P (B) - 2P ( A B )
B )
P = P (B) + P (C) - 2P ( B C )
C )
P = P (C) + P (A) - 2P ( C A )
A )
3 P = 2 (P(A) + P(B) + P(C)) - 2P(A B) + P(A
B) + P(A  B) + P(C
B) + P(C  A))
A))
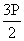 P(A) + P(B) + P(C)[ ( A
P(A) + P(B) + P(C)[ ( A  B) + P(B
B) + P(B C) +P(C
C) +P(C A) ]
A) ]
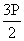 + [ P(A
+ [ P(A B) + P(B
B) + P(B C) +P(C
C) +P(C A) ] P(A) + P(B) + P(C) ...........(1)
A) ] P(A) + P(B) + P(C) ...........(1)
P(A B
B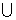 C) = P(A) + P(B) + P(C) - [ P(A
C) = P(A) + P(B) + P(C) - [ P(A B) + P(B
B) + P(B C) + P(C
C) + P(C A) + P(A
A) + P(A B
B C)........(2)
C)........(2)
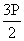 + P (A
+ P (A B
B C) = P(A
C) = P(A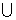 B
B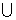 C)
C)
If A, B and C are exhaustive .
then P(A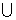 B
B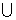 C)=P(A) + P(B) + P(C) holds -
C)=P(A) + P(B) + P(C) holds -
From eqn ........... (2)
P(A B
B C) = P(A
C) = P(A B) + P(B
B) + P(B C) + P(C
C) + P(C A)
A)
P utting in eqn ............ (1)
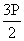 + P(A
+ P(A B
B C) = P(A
C) = P(A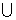 B
B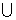 C)
C)
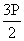 + P2 = 1 ..............(3)
+ P2 = 1 ..............(3)
On solving
P =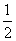
Q. 2. 12 face cards are removed from 52 cards and remaining 40 cards are well shuffled and 4 cards are drawn from pack of 40 cards. Find the chance that all four are of different suit and different denomination .
Ans- Heart Diamond club spade
n(s) = 40 C4
No. of way drawing Ist card = 40 ways
No. of way drawing 2nd card = 27 ways
No. of way drawing 3rd card = 16 ways
No. of way drawing 4th card = 7 ways
Total no. of way of drawing all 4 cards = 40 X 27 X 16 X 7
Dumb question - Why NO. of ways of drawing 2nd card is 27 ?
Ans- Let Ist card drawn is ace of Heart. So, no, Heart and no ace card is further selected. So remaining cards are (40 - 10 - 3) = 27
So, 27 ways
P(E)= i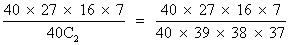
Q. 3 - There are two luts of article one lot contains 3 defective and 5 good article and other lot contains 4 defective and 8 good articles. A lot is randomly seleste a and 3 articles are drawn . this lot will be rejected if 2 or mor than 2 article are found to be defective. Find the chance that this be rejected.
And - E1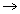 Ist lot is chosen
Ist lot is chosen
E2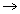 2nd lot is chosen
2nd lot is chosen
E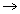 lot is rejected
lot is rejected
P(E) = P(E1) P(E/E1) + P(E2). P(E/E2)
P(E1) = P(E2) = 1/2 (equally likely events)
P(E)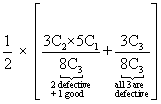 +
+ 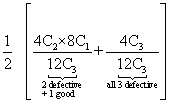
Q. 4 A boy contains | coin of worth M rupees and n coins of total . Worth of M rupees. Coins are drawn without replace -ment till coin whose valime is M, is drawn, I Find the expectaion of draw .
Ans - P(drawing M in Ist draw) =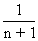
P(drawing M in 2nd) drawn) =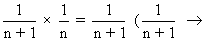 other coin draw,
other coin draw, 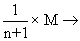 drawing of M)
drawing of M)
P(drawing M in (r + 1)th draw) =
Expectation =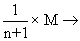 M coin draw In Istdraw, +
M coin draw In Istdraw, + 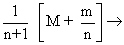 Mcoin draw in IInd draw , +
Mcoin draw in IInd draw , + 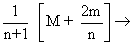 In 3rd draw
In 3rd draw
=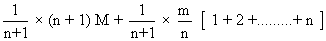
=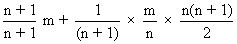
Expectation =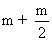
Q. 5 - A letter is known to khave either from Agra or from Mathura or. Satara. on the stamp two consecultive word 'RA'are legible. Find the chance that letter from Agra .
Ans- A : .Two consecutive word 'RA'are legible .
B1: . letter is from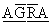
B2: . letter is from
B3: . letter is from
P(B1) = P(B2) = P(B3) =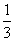
P(B/B1) =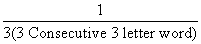 =
= 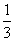
P(A/B2) = 1/6. P(A/B2) = 1/5.
P(A) = P(B1). P(A/B1) + P(B2)+ P(A/B2) + P(B3) P(A/B3)
=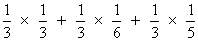
P (B1 / A) =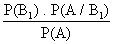
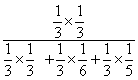
P(B 1 / A) =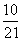
Q. 1- A, B and C are three event such that -
P(exatly one A or B) = P(exactly one B C)
=> P(exactly one C or A) = P
and
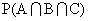 = p2 and A, B and C are
= p2 and A, B and C are exhaustive. Find = value of P .
Ans - Not :- In exhaustive events
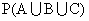 = 1
= 1P = P (a) + P (B) - 2P ( A
 B )
B )P = P (B) + P (C) - 2P ( B
 C )
C )P = P (C) + P (A) - 2P ( C
 A )
A )3 P = 2 (P(A) + P(B) + P(C)) - 2P(A
 B) + P(A
B) + P(A  B) + P(C
B) + P(C  A))
A))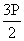 P(A) + P(B) + P(C)[ ( A
P(A) + P(B) + P(C)[ ( A  B) + P(B
B) + P(B C) +P(C
C) +P(C A) ]
A) ]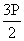 + [ P(A
+ [ P(A B) + P(B
B) + P(B C) +P(C
C) +P(C A) ] P(A) + P(B) + P(C) ...........(1)
A) ] P(A) + P(B) + P(C) ...........(1)P(A
 B
B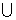 C) = P(A) + P(B) + P(C) - [ P(A
C) = P(A) + P(B) + P(C) - [ P(A B) + P(B
B) + P(B C) + P(C
C) + P(C A) + P(A
A) + P(A B
B C)........(2)
C)........(2)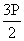 + P (A
+ P (A B
B C) = P(A
C) = P(A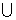 B
B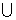 C)
C) If A, B and C are exhaustive .
then P(A
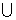 B
B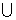 C)=P(A) + P(B) + P(C) holds -
C)=P(A) + P(B) + P(C) holds - From eqn ........... (2)
P(A
 B
B C) = P(A
C) = P(A B) + P(B
B) + P(B C) + P(C
C) + P(C A)
A)P utting in eqn ............ (1)
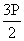 + P(A
+ P(A B
B C) = P(A
C) = P(A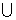 B
B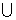 C)
C) 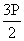 + P2 = 1 ..............(3)
+ P2 = 1 ..............(3)On solving
P =
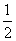
Q. 2. 12 face cards are removed from 52 cards and remaining 40 cards are well shuffled and 4 cards are drawn from pack of 40 cards. Find the chance that all four are of different suit and different denomination .
Ans- Heart Diamond club spade
n(s) = 40 C4
No. of way drawing Ist card = 40 ways
No. of way drawing 2nd card = 27 ways
No. of way drawing 3rd card = 16 ways
No. of way drawing 4th card = 7 ways
Total no. of way of drawing all 4 cards = 40 X 27 X 16 X 7
Dumb question - Why NO. of ways of drawing 2nd card is 27 ?
Ans- Let Ist card drawn is ace of Heart. So, no, Heart and no ace card is further selected. So remaining cards are (40 - 10 - 3) = 27
So, 27 ways
P(E)= i
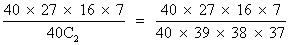
Q. 3 - There are two luts of article one lot contains 3 defective and 5 good article and other lot contains 4 defective and 8 good articles. A lot is randomly seleste a and 3 articles are drawn . this lot will be rejected if 2 or mor than 2 article are found to be defective. Find the chance that this be rejected.
And - E1
 Ist lot is chosen
Ist lot is chosenE2
 2nd lot is chosen
2nd lot is chosenE
 lot is rejected
lot is rejectedP(E) = P(E1) P(E/E1) + P(E2). P(E/E2)
P(E1) = P(E2) = 1/2 (equally likely events)
P(E)
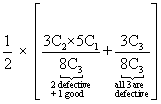 +
+ 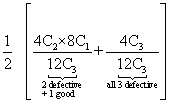

Q. 4 A boy contains | coin of worth M rupees and n coins of total . Worth of M rupees. Coins are drawn without replace -ment till coin whose valime is M, is drawn, I Find the expectaion of draw .
Ans - P(drawing M in Ist draw) =
P(drawing M in 2nd) drawn) =
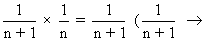 other coin draw,
other coin draw, 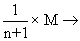 drawing of M)
drawing of M)P(drawing M in (r + 1)th draw) =
Expectation =
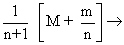 Mcoin draw in IInd draw , +
Mcoin draw in IInd draw , + 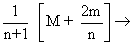 In 3rd draw
In 3rd draw=
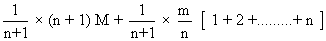
=
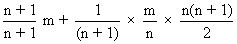
Expectation =
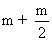
Q. 5 - A letter is known to khave either from Agra or from Mathura or. Satara. on the stamp two consecultive word 'RA'are legible. Find the chance that letter from Agra .
Ans- A : .Two consecutive word 'RA'are legible .
B1: . letter is from
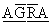
B2: . letter is from

B3: . letter is from

P(B1) = P(B2) = P(B3) =
P(B/B1) =
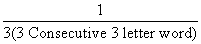 =
= 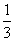
P(A/B2) = 1/6. P(A/B2) = 1/5.
P(A) = P(B1). P(A/B1) + P(B2)+ P(A/B2) + P(B3) P(A/B3)
=
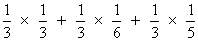
P (B1 / A) =
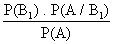
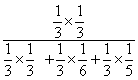
P(B 1 / A) =