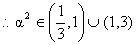Progression - 3

Some Special Series:
1) .

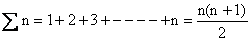Why?

This is an A.P with a =1 and d=1

So,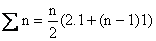

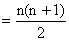
2)

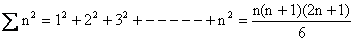
Proof:

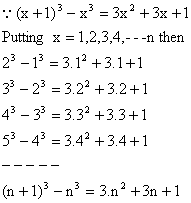
Adding all we get,

3)

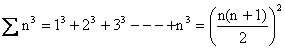
Proof:

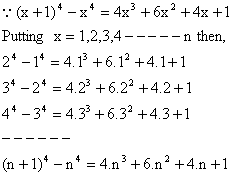
Adding all we get,

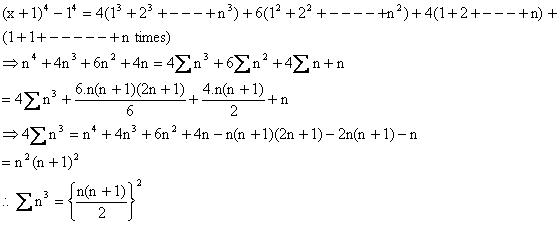
Illustration 9:

If S₁, S₂, S₃, ------- S_n are the sums of infinite geometric series whose first term are 1, 2, 3, --------n and whose common ratios are 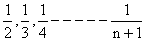respectively then find the value of .

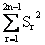Solution:

The r^th series has the first term a = r.

Common ratio = 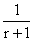, Sum = S_r.

Some Special Series: 
1) Method of Difference:
Suppose a₁, a₂, a₃--------- is a sequence such that sequence a₂-a₁, a₃-a₂, -------- is either an A.P or a G.P. Then n^th term of this sequence may be found as follows:

Let

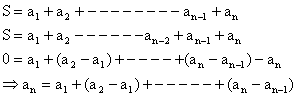
So, we find value of a_n and hence S_n.

 

Dumb Question:
1)      How do we ensure that value of a_n can be calculated?

Ans: The terms 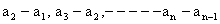form either an A.P or a G.P. So we can always sum them up.

2) Method of V_n:

Let T₁, T₂, T₃------- be terms of a sequence. If there exists a sequence V₁, V₂, V₃---------- Satisfying 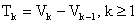then,

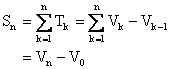
Illustration 10:

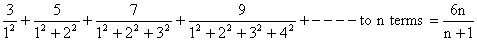. Then find the sum to infinite terms of the series on the left hand side.

Solution:

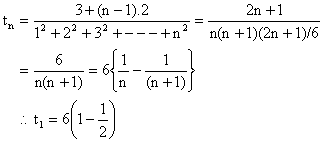
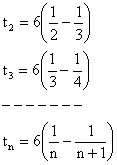
Adding L.H.S =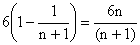

Thus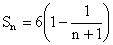

\ Sum of infinite terms

                                                 PROBLEMS (EASY TYPE)

1) If the roots of the equation 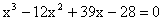are in A.P then what will be their common difference?

Solution:

Sum of three numbers a-d, a, a+d are in A.P.

= 3a = 12

\ a = 4 is a root of cubic

\ (x-4) (x²-8x+7) = 0

\ x = 1, 4, 7 or 7, 4, 1 and d = ±3.

2) The sum of the squares of three distinct real numbers which are in G.P is S² if their sum is aS, show that .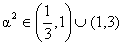

Solution: Let the three numbers in G.P is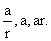

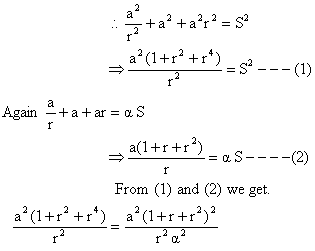
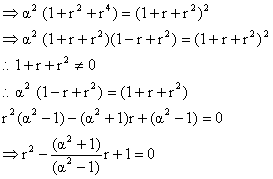
Since r is real 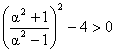{the number in G.P are different}.

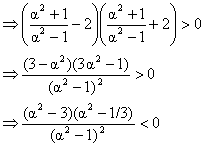
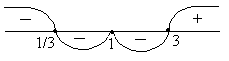
                    Fig (1)

Critical points of a² are 1/3, 3, 1 from wavy curve method.