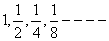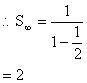3) Find the sum
1.2.3.4.5+2.3.4.5.6+3.4.5.6.7+-------+ (n-4) (n-3) (n-2) (n-1) n
Solution:
The given sum =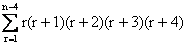 
3) Prove that natural number 7.7.7------7 consisting of seven is a composite number divisible by a multiple of 7.
Solution:
7.7.7------7 = 7´1.1.1----1
= 7´integer´integer.
4) If a, b, c are in H.P and b, c, d are in G.P and c, d, e are in A.P show that
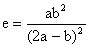
Solution:
Given a, b, c are in H.P
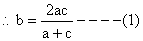
b, c, d are in G.P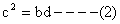 
And c, d, e are in A.P
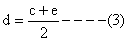
We want the relation in a, b, e
Then eliminate c, d from (1), (2) and (3)
From (1) ab+bc = 2ac
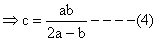
From (3) and (4)
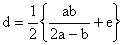
Substituting the values of c and d from (4) and (5) in (2) we get,
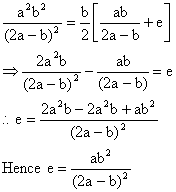
5) Balls are arranged in rows to form an equilateral triangle the first row consist of one ball, the second row of two balls and so on. If 669 more balls are added then all the balls can be arranged in the shape of a square and each of the sides then contains 8 balls less than each side of the triangle then find the initial number of balls.
Solution:
S = 1+2+3+4+-------+n =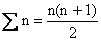 
S+669 = (n-8)2 by given condition
Or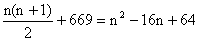 
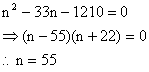
\ S = 1540.
Check: 1540+669 = 2209 = (55-8)2 = (47)22222233322222.
6) The equation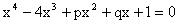 
has four positive roots then find the value of (p, q).
Solution: Let the roots be a,b, g, d.
\ a+ b+ g+ d = 4. and a.b.g.d = 1.
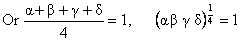
\ A.M = G.M of the roots
\ All the roots are equal and each equal to 1.
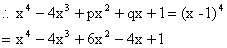
Comparing we get p = 6, q = -4.
7) If a1, a2, a3, --------- an are in A.P where ai ¹ kp for all i, prove that
Cosec a1.Cosec a2 + Cosec a2.Cosec a3 + --------+Cosec an-1.Cosec an =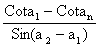 
Solution:
L.H.S =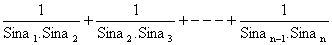 
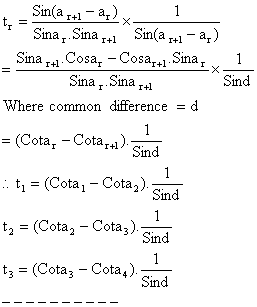
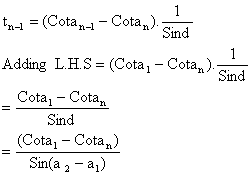
8) Prove that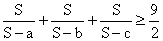 
if S = a+b+c [a, b, c>0].
Solution:
We have to prove
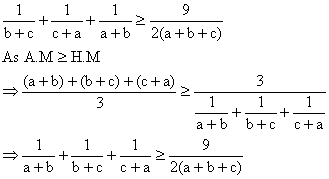
9) Two consecutive numbers from 1, 2, 3-------n are removed. Arithmetic mean of the remaining numbers is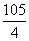 
. Find n and those removed number.
Solution:
Let p and (p+1) be removed numbers from 1, 2, 3, ------ n then sum of remaining numbers.
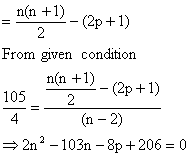
Since n and p are integers so n must be even let n=2r.
We get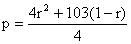 
Since p is an integer then (1-r) must be divisible by 4.
Let r = 1+4t we get
n = 2+8t and p = 16t2-95t+1.
Now 1£p<n.
Þ 1£ 16t2-95t+1< 8t+2.
Þ t = 6.
Þ n = 50 and p = 7.
Hence removed numbers are 7 and 8.
10) Find the sum of infinitely decreasing G.P whose third term, the triple product of the first term by the fourth term A.P with the common difference equal to 1/8.
Solution:
Let G.P be a, ar, ar2------ Since the G.P is infinite and decreasing -1< r< 1 and r>0, so 0< r<1 and so a>0 according to the hypothesis.
ar2, 3a ar3, ar are in A.P with common difference 1/8.
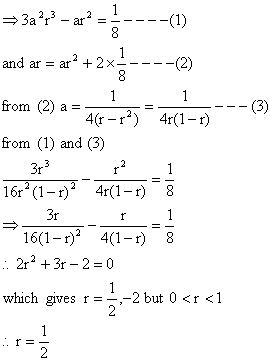
From (3) we get a = 1
Hence G.P is 
