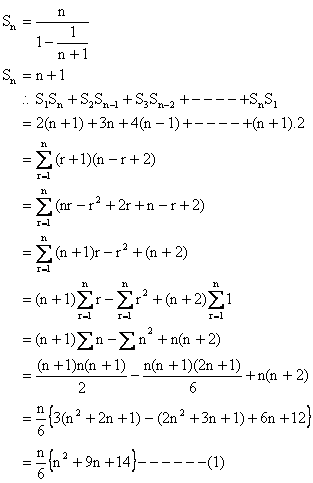Progression - 5
PROBLEMS (MEDIUM TYPE)
1) A sequence a1, a2, a3, ------- an of real numbers is such that a1= 0, |a2| = |a1+1|, |a3| = |a2+1|, ---------- |an| = |an-1+1|. Prove that arithmetic mean of a1, a2, -------- an can not be less than -1/2.
Solution:
Let us add one more number an+1 to the given sequence. The number an+1 is such that |an+1| = |an+1|.
Squaring all numbers we have,
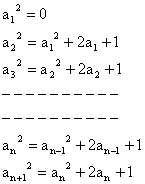
Adding the above equalities we get,

Dumb Question:
1) Why ![]() ?
?
Ans: an+1 is given to be a real no in the question and hence ![]() is going to be a positive number.
is going to be a positive number.
There fore ![]() .
.
2) There are (4n+1) terms in a certain sequence of which the first (2n+1) terms form an A.P of common difference 2 and the last (2n+1) terms are in G.P of common ratio 1/2. If the middle terms of both A.P and G.P be the same what is the mid term of this sequence.
Solution: d=2, r=1/2
If there be odd number of terms then mid term = ![]() .
.
T2n+1 is the mid term of sequence of (4n+1) odd terms a+2nd = a+4n ------ (1)
This mid term is the last term of A.P and first term of following G.P. Each of (2n+1) terms with this term being common to both.
Tn+1 and tn+1 are mid terms of A.P and G.P
Tn+1 = a+nd = a+2n.
![]()
By given condition Tn+1= tn+1.
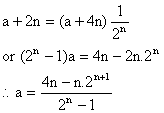
Hence mid term of sequence by (1) is
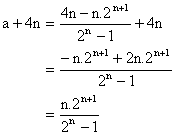
Dumb Question:
1) Why middle term of the G.P is ![]() ?
?
Ans: Well the first term of the G.P is the last term of the A.P
So, the first term = a+2(2n+1-1)
= a+4n.
Now the (n+1)th term of the G.P is
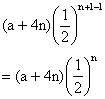
3) If ![]() then find
then find ![]() .
.
Solution:

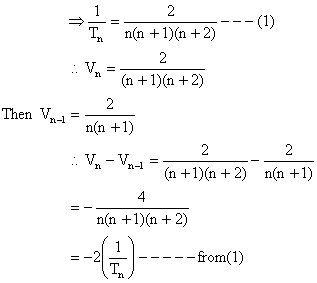
![]()
Putting n = 1, 2, 3, ------n
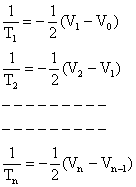
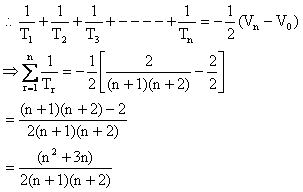
4) Evaluate sum of n terms of the series ![]()
Solution:
![]()
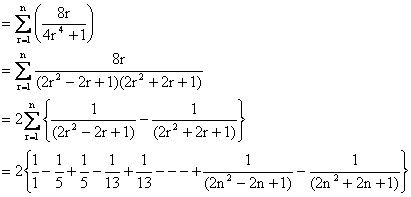
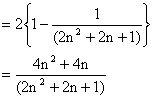
5) Find the sum of 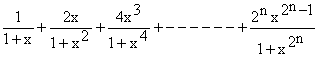
Solution:
If S be the sum then consider ![]()
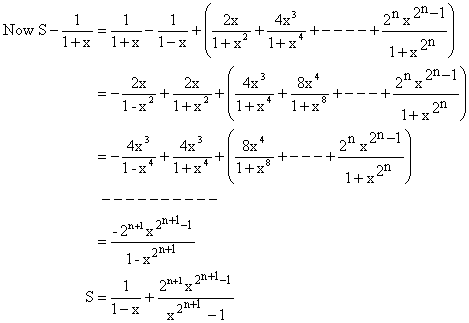
6) If 2a+b+3c = 1 and a>0, b>0, c>0 find the greatest value of ![]() and obtain the corresponding values of a, b, c.
and obtain the corresponding values of a, b, c.
Solution:
Consider the positive numbers ![]() {As there is a4, take 4 equal parts of 2a; as there is b2 take 2 equal parts of b; as there is c2 take 2 equal parts of 3c}.
{As there is a4, take 4 equal parts of 2a; as there is b2 take 2 equal parts of b; as there is c2 take 2 equal parts of 3c}.
For the numbers,
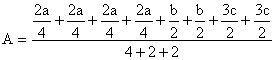
![]()
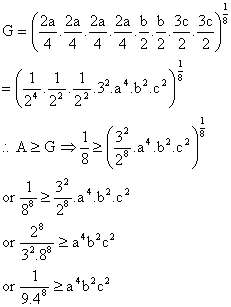
So the greatest value of ![]() =
= ![]()
Now when the value is greatest the numbers themselves have to be equal.
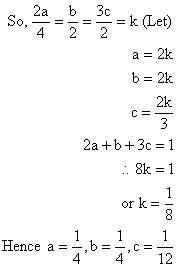
7) If ![]() where xÎR then find
where xÎR then find ![]() .
.
Solution:

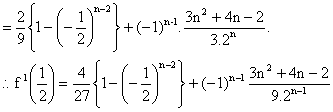
8) Let Sn, n=1, 2, 3, ------- be the sum of infinite geometric series whose first term is n and the common ratio is ![]() evaluate.
evaluate.
![]()
Solution: