Progression - 6

And

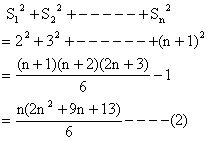
From (1) and (2) we get,

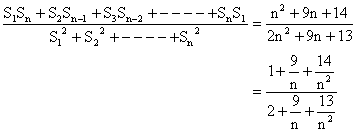
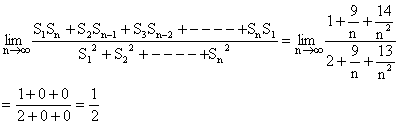
Dumb Question:

1)

Ans:

S_n is n+1

So, S_r = r+1.

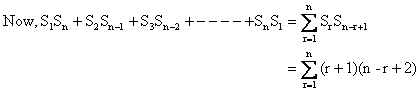
9) Prove that the numbers of the sequence 121, 12321, 1234321, ----- are each a perfect square of odd integer.

Solution:

We have first term T₁ = 121 = 10² + 2´10 + 1

Second Term T₂ = 12321 = 10⁴ +2´10³ + 3´10² +2´10+1.

Third Term

------------------------------------------------

n^th term T_n = 123---------- n (n+1) n ---------- 4321

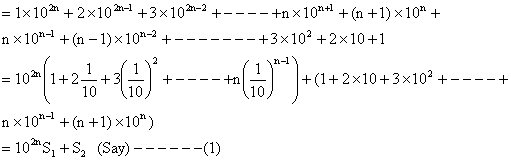
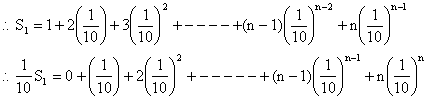
Substracting we get,

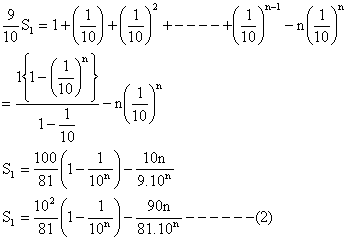
And

Substracting we get,

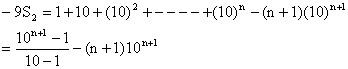
Substituting the values of S₁ and S₂ from (2) and (3) in (1) we get

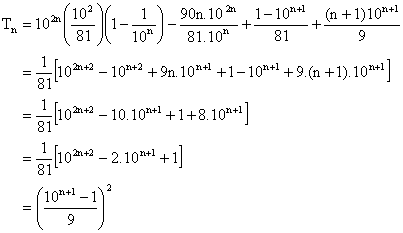
Since sum of digits of is divisible by 9.

is a positive integer.

Thus T_n is a perfect square.

10) Sum to n terms:

Solution:

Regrouping the terms the series becomes

The number of terms in each group will depend on n.

If n=3m i.e. n is divisible by 3

Sum of the first group = 1+4+7+--------- to m terms;

Sum of the second group;

Sum of the third group =

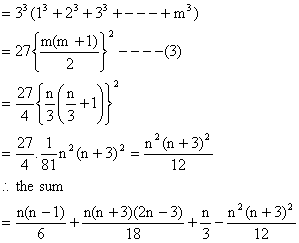
When n is divisible by 3.

If n=3m+1 i.e. When n is divided by 3. The remainder is 1. In this case the first group will have m+1 term while others will have m terms each.

\ In (1) we shall get

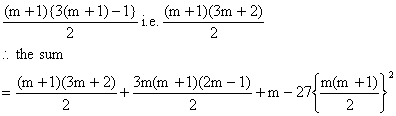
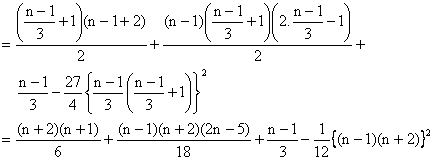
When n is of the form 3m+1.

If n=3m+2 i.e. When n is divided by 3, the remainder is 2. In this case the first and the second group will have (m+1) terms each while the third will have m terms.

\ In (1) we shall get,

In (2) we shall get

There fore the sum

(Using 3)

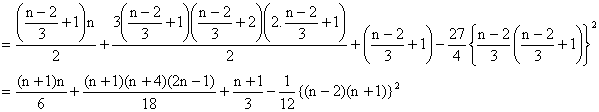
Where n is of the form 3m+2.

Dumb Question:

1)      What was the need of considering three cases where n=3m, 3m+1, 3m+2?

Ans: The need for considering 3 cases arised because the last term of the series to be summed was not known to us the series was essentially three different series so to sum the series this approach of taking 3 different cases was essential.