Illustration 5:
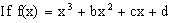and f (0), f (-1) are odd integers then prove that f(x) =0 cannot have all integral roots.
Solution:
f (0) =d, f (-1) = -1+b-c+d
As given in the equation, d is odd and also -1+b-c+d = odd
Or b-c = 1+odd-d
= even-odd
= odd ------------ (1)
So,d and b-c are odd
Now let a, b, g be integral roots
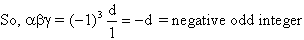
abg are 3 integers whose product is odd.
So, a, b, g are odd.
Again ab+ga+bg = c
And a+b+g = -b
Now b and c will also be odd and so b-c will be even which contradicts (1).
So roots cannot be all integers.
Wavy Curve Method:
Let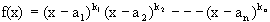 
where 
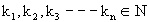and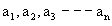 
are fixed numbers satisfying the condition, 
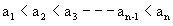First we mark the numbers 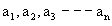on the real axis and the plus sign in interval of the right of the largest of these numbers i.e. on right of an. If kn is even, put plus sign on left of an otherwise put minus sign.
Now in next interval the sign is put according to this rule: When passing through an-1
f (x) changes sign if is odd number otherwise it has same sign. Similar rule is applied for the next interval and so on.
Union of all intervals with plus sign give solution of f (x)>0 and solution of f (x) <0 is union of all intervals in which we put the minus sign.
Illustration 6:
Solve the inequality
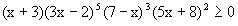
Solution:
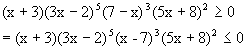
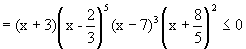
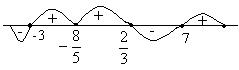
Fig (1)
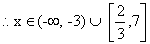
Sign of quadratic expression:
The expression f(x) = y =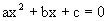 
, a ¹ 0, a, b, cÎR can be written as
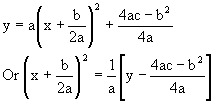
Which represents a parabola with vertex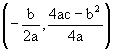 
and axis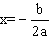 
:
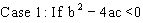1) If a>0
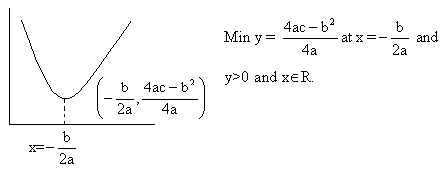
Fig (2)
2) If a<0
Fig (3)
1) If a>0
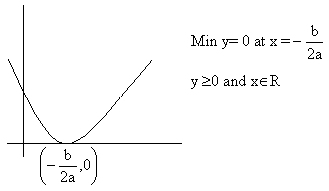
Fig (4)
2) If a<0
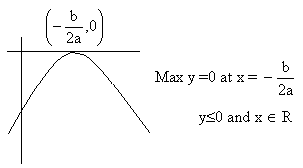
Fig (5)
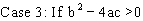
1) If a>0
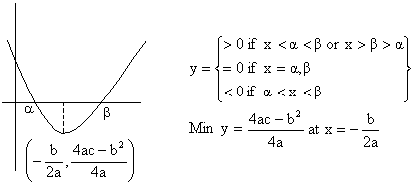
2) If a<0
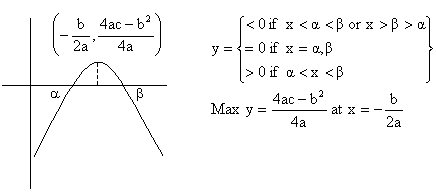
Illustration 7:
Find the condition so that function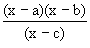 
will assume all real values?
Solution:
y =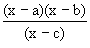
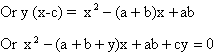
Now the determinant D of this equation must be greater than zero for all values of y
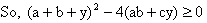
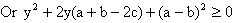
Now in this equation A>0 so B2-4AC should be less than zero i.e. B2-4AC<0 for this condition to hold
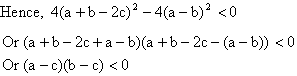
i.e. c lies between a and b.
So, a<c<b if a<b
Or b<c<a if b<a.
Intervals of roots
Let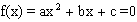 
, a ¹ 0, a, b, cÎR and a>0 suppose k, k1, k2, p, qÎR and k1<k2 then
1) If D³0, f (k)>0 and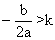 
then both roots of f (x) = 0 are greater than k why?
a>0 and D³0
\Shape of parabola is like this
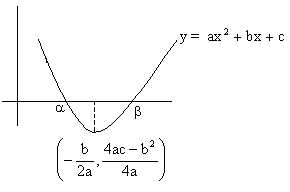
Fig (8)