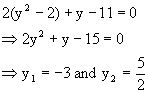Quadratic Equation - 3
Now ![]() , so k is on left hand side of the point
, so k is on left hand side of the point ![]()
Also f (k)>0, so it is possible only when k<a.
So,a, b>k.
1) If D³0, f (k)>0 and ![]() then both roots of f (x) =0 are less than k. Why?
then both roots of f (x) =0 are less than k. Why?
As D³0 and a>0 so shape of parabola is like this
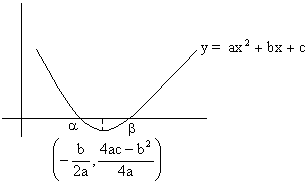
Fig (9)
Now f (k)>0 so k>b or k<a
And also ![]()
So, k<a is ruled out
Therefore k>b
Hence, k>a,b.
2) If D>0 and f (k) <0 then k lies between root of f (x) = 0 why?
D>0 and a>0
So the shape of parabola is
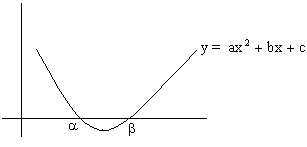
Fig (10)
Now f (k) <0, so clearly a<k<b.
4) If D>0 and f (k1)´f (k2) <0, then exactly one root of equation f (x) = 0 lies in interval (k1, k2). When (k2>k1) Why?
Since f (k1)´f (k2) <0
So, f (k1) and f (k2) should be of opposite sign.
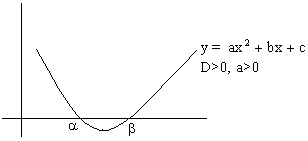
Fig (11)
1) Now let f(k1)<0 and f(k2)>0
So, a<k1<b and k2>b (because k2>k1)
And hence b lies in interval (k1, k2).
2) Second case is f (k1) >0 and f (k2) <0
So, a< k2<b and k1<a (because k2>k1)
Hence a lies in interval (k1, k2).
So exactly one root lies in interval (k1, k2).
5) If D³0, f (p)>0 and f (q)>0, q>p then both the roots of the equation f(x) = 0 will
lie between p and q, if ![]() why?
why?
Suppose both roots lie in interval (p, q)
Now D³0, a>0 therefore shape of parabola is
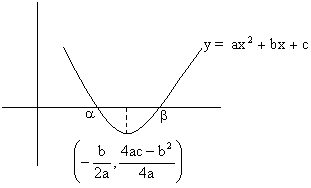
Fig (12)
a, b lies in interval (p, q)
So, b<q and p<a
And hence p<a<b<q
![]()
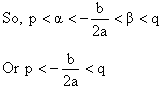
6) If D³0, ![]() and
and ![]() then both roots of the equation f(x) = 0 are positive. Why?
then both roots of the equation f(x) = 0 are positive. Why?
![]()
Also ![]() so, product of root is positive, and hence clearly both roots are positive.
so, product of root is positive, and hence clearly both roots are positive.
Illustration 8:
For what values of ‘a’ exactly one root of the equation ![]() lies between 1 and 2.
lies between 1 and 2.
Solution: Since exactly one root of given equation lie between 1 and 2,
So f (1)´f (2) <0
Here f(x) = ![]()
So, f (1)´f (2) <0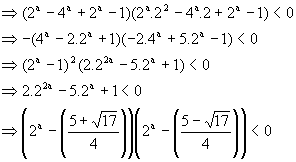
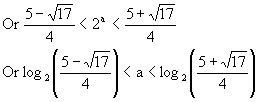
Some important results using differentiability:
![]()
1) If f(x) = 0 has a real root a of multiplicity g (g>1) then f(x) = (x-a)gg (a) where g(a)¹0. Also f(x) = 0 has a as a real root with multiplicity (g-1)
2) If f(x) = 0 has n real roots then f (x) = 0 has (n-1) real roots.
Illustration 9:
A polynomial p(x) has ![]() as one of the factors, other roots of this polynomial lie in the range
as one of the factors, other roots of this polynomial lie in the range ![]() Prove that g(x) where g(x) = p1(x) has at least one positive root.
Prove that g(x) where g(x) = p1(x) has at least one positive root.
Solution:![]()
Now p(x) has a root 2 with multiplicity 2.
So the derivative of p(x), p1(x) or g(x) must has 2 as root with multiplicity 2-1=1.
So g(x) has at least one positive root which is 2.
Easy (Quadratic)
Q-1: The roots of the quadratic equation ![]() are a and b2 Where
are a and b2 Where ![]() then Show that
then Show that ![]() has roots (a+ib)100 and (a-ib)100
has roots (a+ib)100 and (a-ib)100
Solution: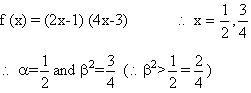
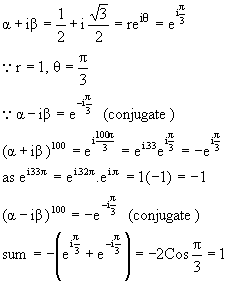
Product = 1.![]() Required equation is
Required equation is ![]()
Q-2: If a, b are the roots of the equation ![]() then prove that
then prove that 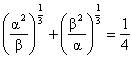
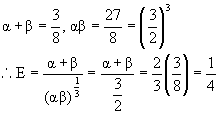
Q-3: If ![]() then find value of expression
then find value of expression ![]() .
.
Solution:
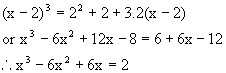
Q-4: Solve the equation ![]()
Solution:
Since x=0 is not a solution of given equation. Dividing by x2 in both sides of (1) we get,
![]()
Putting ![]() in equation (2) then (2) reduces in the form,
in equation (2) then (2) reduces in the form,