Consequently the original equation is equivalent to the collection of equations, 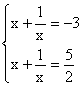
We find that 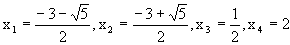
Q-5: If aÎz and the equation (x-a) (x-10) +1=0 has integral roots, then what is the value of ‘a’? Solution: As both x and a are integers and hence given equation implies that either x-a =1 and x-10= -1 or x-a = -1 and x-10=1.  x=9 and hence a=8 or x=11 and a=12. x=9 and hence a=8 or x=11 and a=12.
Therefore possible values of a’s are 8, 12. Q-6: Find the values of ‘a’ for which inequality  is true for at least one is true for at least one 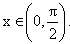 Solution: The required condition will be satisfied if – The quadratic expression (quadratic in tanx).
1) f (x) =  has positive discriminant and , has positive discriminant and ,
2) At least one root of f(x) =0 is positive as tanx>0, for all 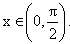
For (1) discriminant >0

For (2) we first find the condition, that both the roots of 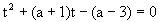
(t=tanx) are non positive for which,
Sum of roots<0, product of roots 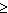 0 0
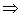 - (a+1) <0 and – (a-3) - (a+1) <0 and – (a-3) 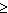 0 0 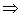 -1 <a -1 <a 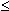 3 3
Condition (2) will be fulfilled of a 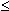 -1or a>3 - - - - - - - - - -(b) -1or a>3 - - - - - - - - - -(b)
Required value of a is given by intersection of (a) and (b) Hence 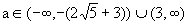 Q-7: Solve the equation- 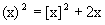 where (x) and [x] are the integer just less than or equal to x and just greater than or equal to x respectively. where (x) and [x] are the integer just less than or equal to x and just greater than or equal to x respectively. Case 1: If x 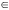 I, I, Then (x) = [x] - - - - - - - - (1), 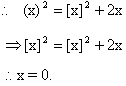
Case 2: if x 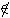 l l
Then (x) = [x]-1
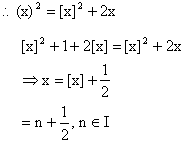
Hence the solution of original equation is, x=0, 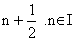 . .
Q-8: If the equation 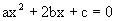 has real roots a, b, c being real numbers and if m and n are real number such that m2>n>0 then prove that the equation has real roots a, b, c being real numbers and if m and n are real number such that m2>n>0 then prove that the equation 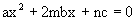 has real roots. has real roots. Solution: Since roots of the equation 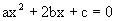 are real are real

and discriminant of 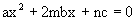 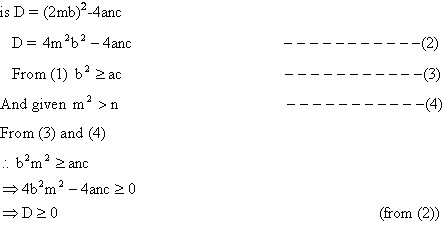
Hence roots of equation 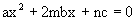 are real. are real.
Q-9 If graph of function 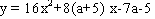 is strictly above the x-axis then show that -15<a<-2 is strictly above the x-axis then show that -15<a<-2
Solution: Y has to be positive
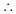 16x2+8(a+5) x-(7a+5) = +ve 16x2+8(a+5) x-(7a+5) = +ve
 Since sign of first term is +ve therefore the expression will be +ve if D<0. Since sign of first term is +ve therefore the expression will be +ve if D<0.
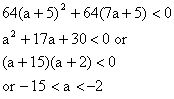 Q-10: For real roots what is the solution of the equation 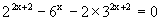
Solution: 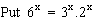
Divide by 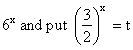 where t is +ve being exponential function. where t is +ve being exponential function.
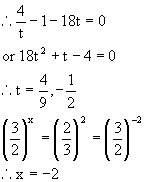
The other value 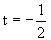 is rejected as t is +ve. is rejected as t is +ve. Q-11: Obtain a quadratic expression in x and solve for it if
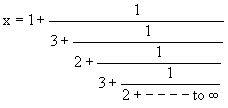
Here 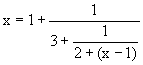 Because, 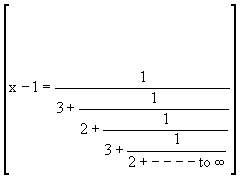 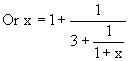
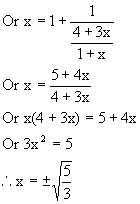
But clearly x is positive
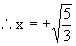
Q-12: Solve for x 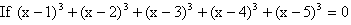 Solution: Here A.M of {x-1, x-5} =A.M of {x-2, x-4} =x-3, put x-3=y then, x-1= y+2, x-2=y+1, x-4=y-1, x-5=y-2.
 The equation becomes, The equation becomes,
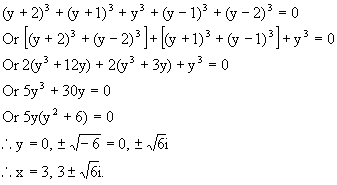
|