Quadratic Equation - 6
The corresponding equation in q is
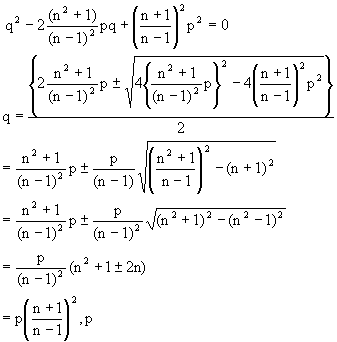
The sign scheme for (3) is as shown
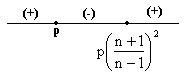
(3) 
q can not lie between 
Subsequently:
a) If a>1 then system (2) has no solutions, and therefore the original equation has no solution.
b) If a=1, then system (2) has only unique solution i.e. x= -1 and the conditions of the original equation are not satisfied. Hence the original equation has no solution.
c) If 0<a<1 then -1<-a<0 and therefore the interval [-a-2, -a] contains no less than four integers provided the inequality -a-2£ -4 holds true. Now solve the system.
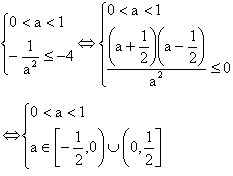
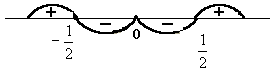
Fig (16)
Thus 
, then the given equation has no less than four different integer solutions.
d) If -1<a<0 then 0<-a<1 and therefore the interval [-a-2, -a] contains no less than four integer provided the inequality -a-2 £ -3 holds true. Now solve the system.
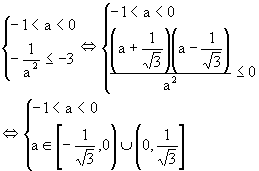
Thus 
, then the given equation has no less than four different integer solutions.
Q-2: Find all values of a for which the equation 
has no less than four different integer solution.
Solution: The given equation can be written in the form,
The given equation is equivalent to the system,
The equation |A|+|B| = A-B
Holds true 
0 and B 
0
Now consider following cases
Case 1: If a=0
Then system (1) gives equation have all xÎR as their solutions.
Fig (17)
Case 2: If a ¹0 then system (1) is equivalent to
Now,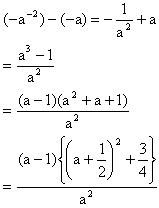
For a<1, a 0
-a-2+a<0
For a=1
-a-2+a=0
For a>1
-a-2+a>0
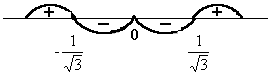
Fig (18)
e) If a= -1 then the interval [-1, 1] contains only three integer i.e. condition of the problem are not satisfied.
f) If a<-1 then -1<-a-2<0 and therefore the interval [-a-2, -a] contains no less than four integers. It is necessary that the inequality –a ³ 3 hold true thus for a £ -3 the given equation has no less than four integer solutions.
Combining all the results we get the set of required values for a,
Q-3: Solve for x
Solution:
Here,
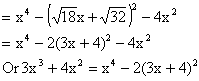
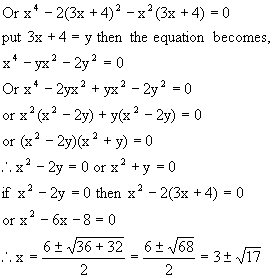
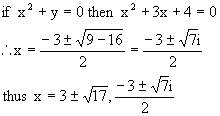
- Quadratic
- Root
- Discreminant
- Polynomial
- Coefficient
- Common roots
- Lagrange’s Identity
- Cauchy Swartz Inequality
- Multiplicity