SHM -2
Now suppose the ball started from a point after than 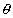 = 0 say
= 0 say 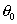 then :
then :
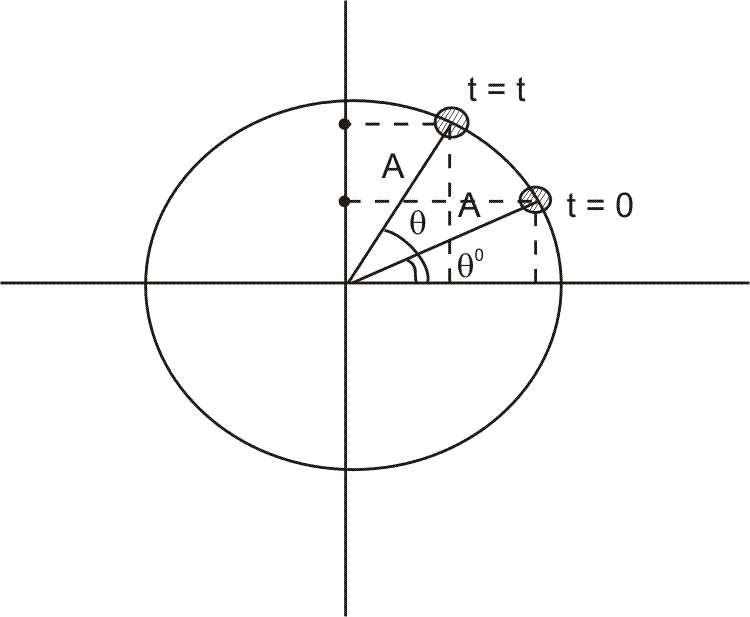
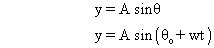
So here
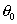 = phase constant
= phase constant
# illustration :-
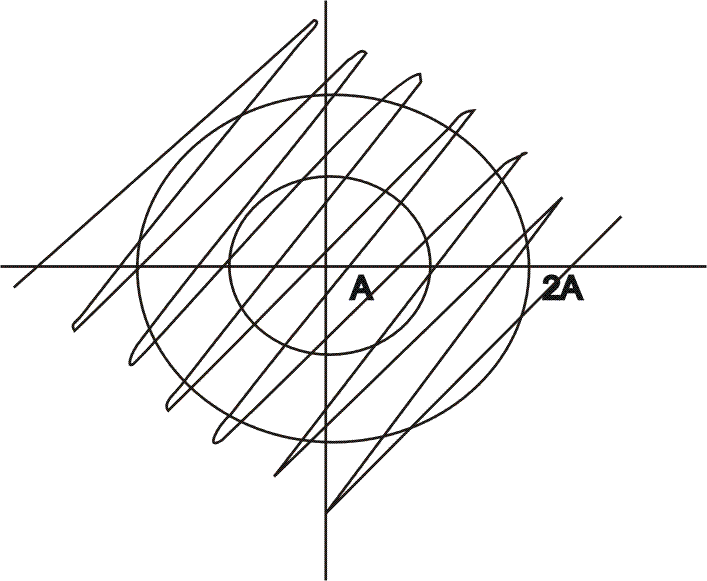
Two SHM's of amplitude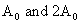 with initial hase constanta as
with initial hase constanta as 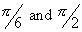 start with angular velocities w and 4w respectively. Find the time after which they are in phase.
start with angular velocities w and 4w respectively. Find the time after which they are in phase.
Question:-
That they are in phase.
Solution :- "In phase" means having same phase. Which means they are at the same position instant & their velocities are also in same direction.
* Tip The problem can be solved easily using two techniques : (1) circle method for SHM
(2) Relative Concept.
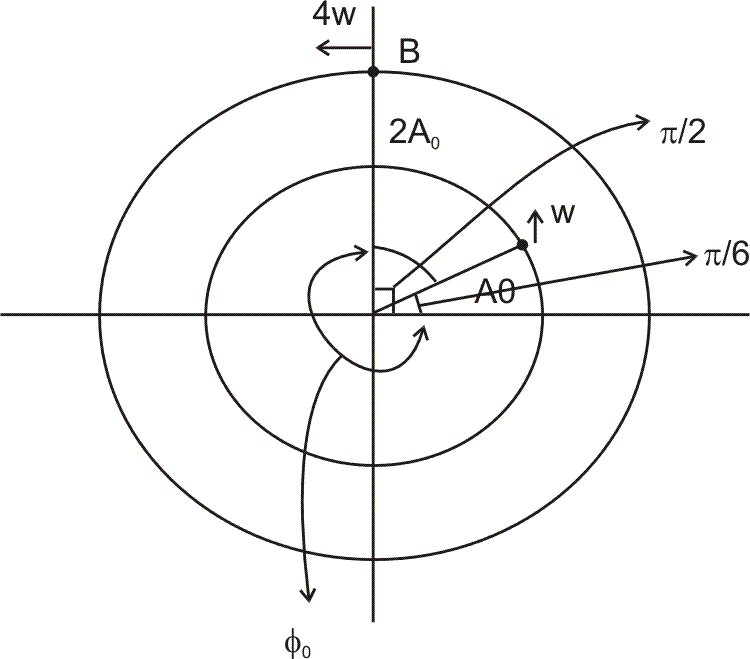
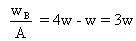
Initial angle between two =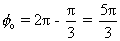
So time taken =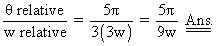
Dumb Question : Is only the functiony =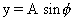 SHM?
SHM?
Solution :- No, any function which satiesfies the condition that if y = y(t); then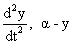 , can represent the SHM.
, can represent the SHM.
Accelaration and velocity in SHM :
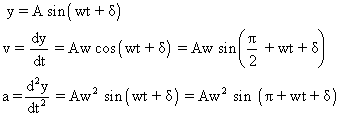
if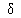 = 0 and
= 0 and 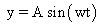
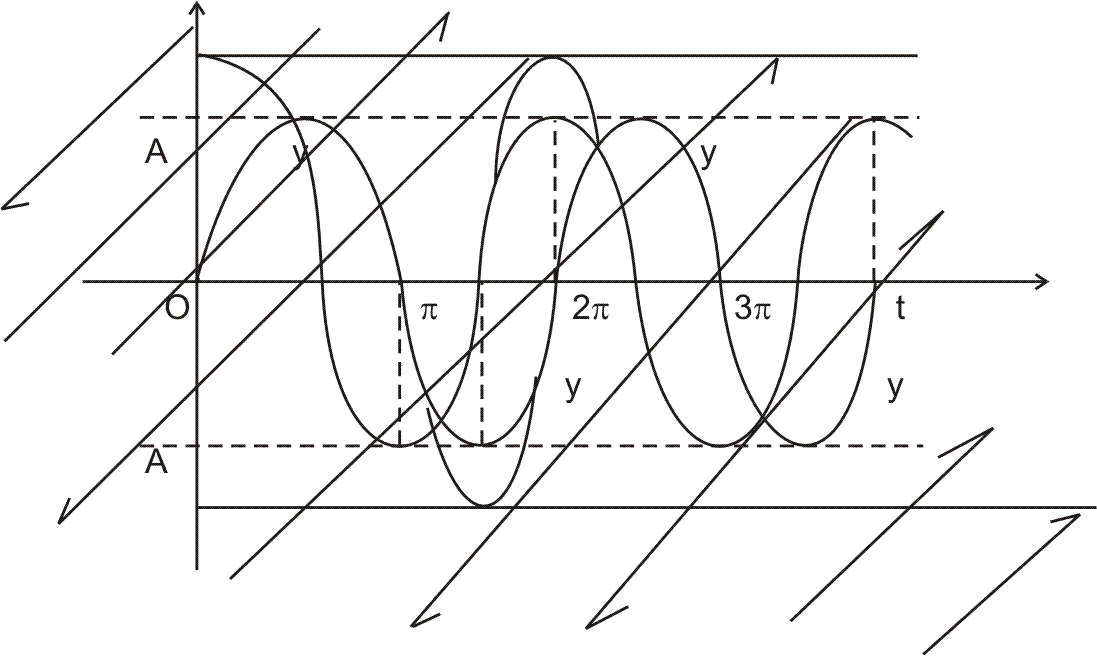
The graphs if drawn are :-
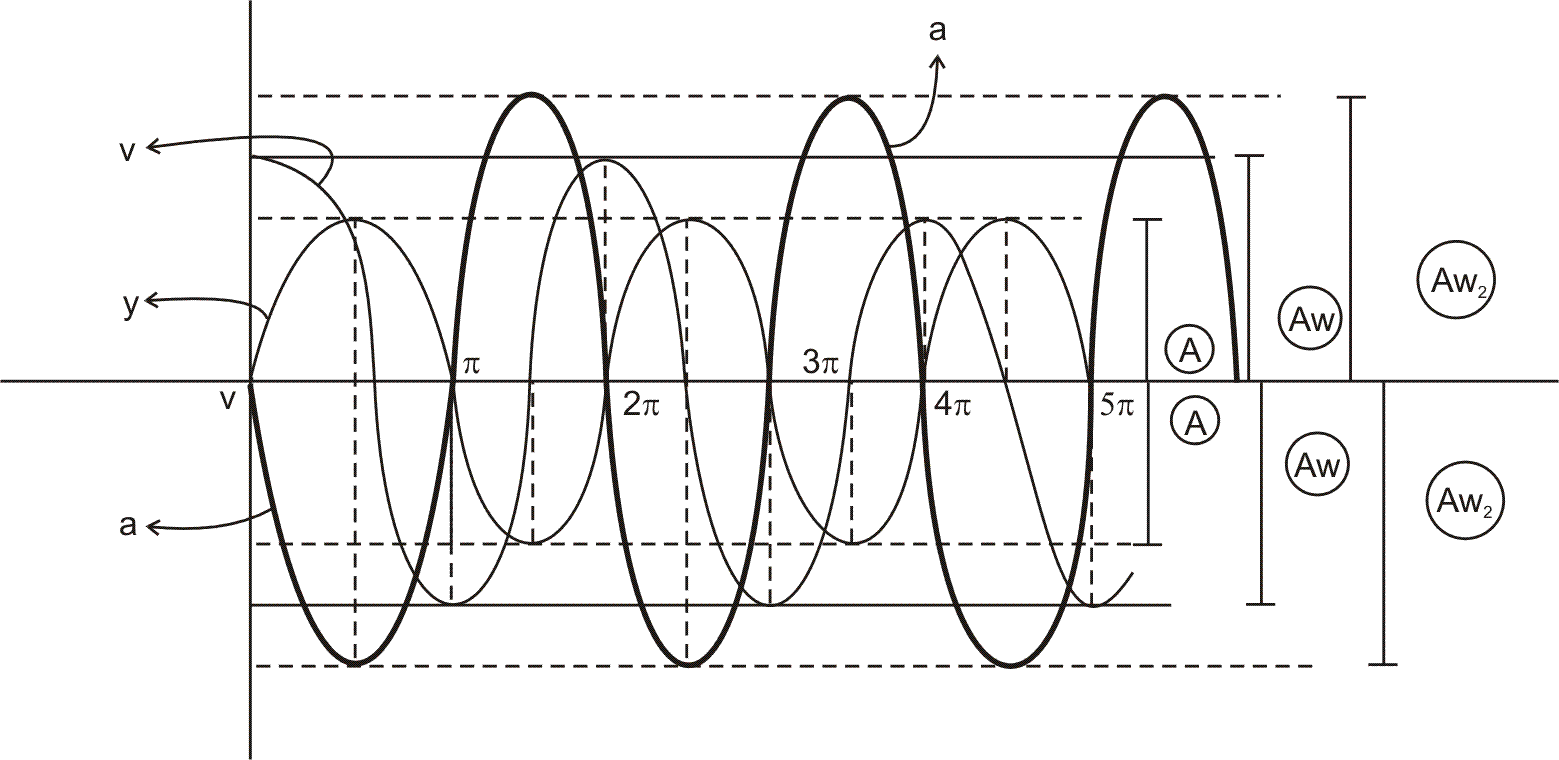
[of = 0] . All v, y, w have different Amplitude.
= 0] . All v, y, w have different Amplitude.
Differential Equation of accelation of particle SHM is
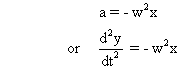
# Illustration : If equation of a motion is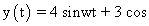 Show that it is SHM and find maximum accelaration and maximum velocity.
Show that it is SHM and find maximum accelaration and maximum velocity.
Solution :-
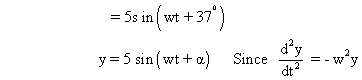
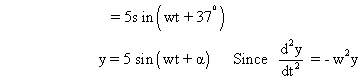
Hence it is SHM.
Now
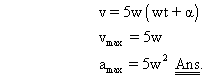
* Energy terms in SHM :

(a) Kinetic Energy :
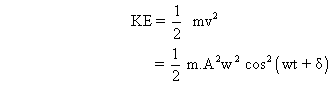
(b) Potential Energy :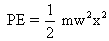
Derivation : Work done by Force F during displacement from x to x + d is
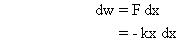
Integrate both sides
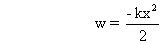
Now Potential Energy = - Work Done by force.
Potential Energy = - Work Done by force.
So,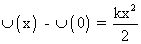
Let at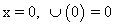
So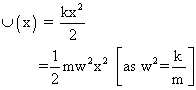
So total Energy in SHM :
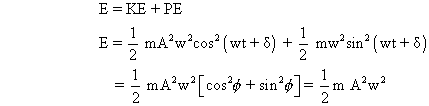
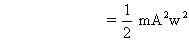 for a particular SHM with w
for a particular SHM with w
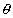 = 0 say
= 0 say 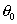 then :
then :
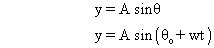
So here
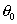 = phase constant
= phase constant# illustration :-

Two SHM's of amplitude
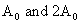 with initial hase constanta as
with initial hase constanta as 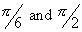 start with angular velocities w and 4w respectively. Find the time after which they are in phase.
start with angular velocities w and 4w respectively. Find the time after which they are in phase.Question:-
That they are in phase.
Solution :- "In phase" means having same phase. Which means they are at the same position instant & their velocities are also in same direction.
* Tip The problem can be solved easily using two techniques : (1) circle method for SHM
(2) Relative Concept.

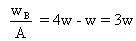
Initial angle between two =
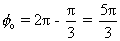
So time taken =
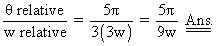
Dumb Question : Is only the functiony =
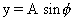 SHM?
SHM?Solution :- No, any function which satiesfies the condition that if y = y(t); then
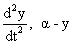 , can represent the SHM.
, can represent the SHM.Accelaration and velocity in SHM :
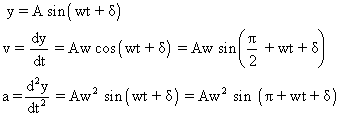

if
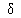 = 0 and
= 0 and 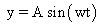
The graphs if drawn are :-

[of
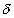 = 0] . All v, y, w have different Amplitude.
= 0] . All v, y, w have different Amplitude.Differential Equation of accelation of particle SHM is
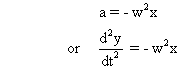
# Illustration : If equation of a motion is
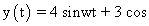 Show that it is SHM and find maximum accelaration and maximum velocity.
Show that it is SHM and find maximum accelaration and maximum velocity.Solution :-
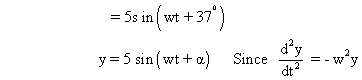
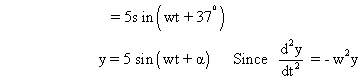
Hence it is SHM.
Now
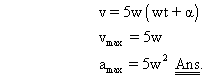
* Energy terms in SHM :

(a) Kinetic Energy :
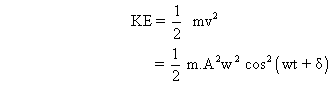
(b) Potential Energy :
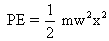
Derivation : Work done by Force F during displacement from x to x + d is
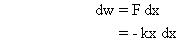
Integrate both sides
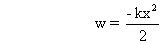
Now
 Potential Energy = - Work Done by force.
Potential Energy = - Work Done by force.So,
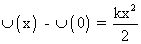
Let at
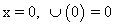
So
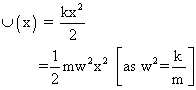
So total Energy in SHM :
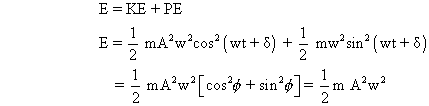
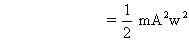 for a particular SHM with w
for a particular SHM with w