SHM -3

* Note :- (K.E.) + (P.E.) = Const. =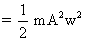
So we can say that if
Dumb Question :- What is the relevance of Mechanical energy being constant hare ?
Solution :- Suppose the system i like :


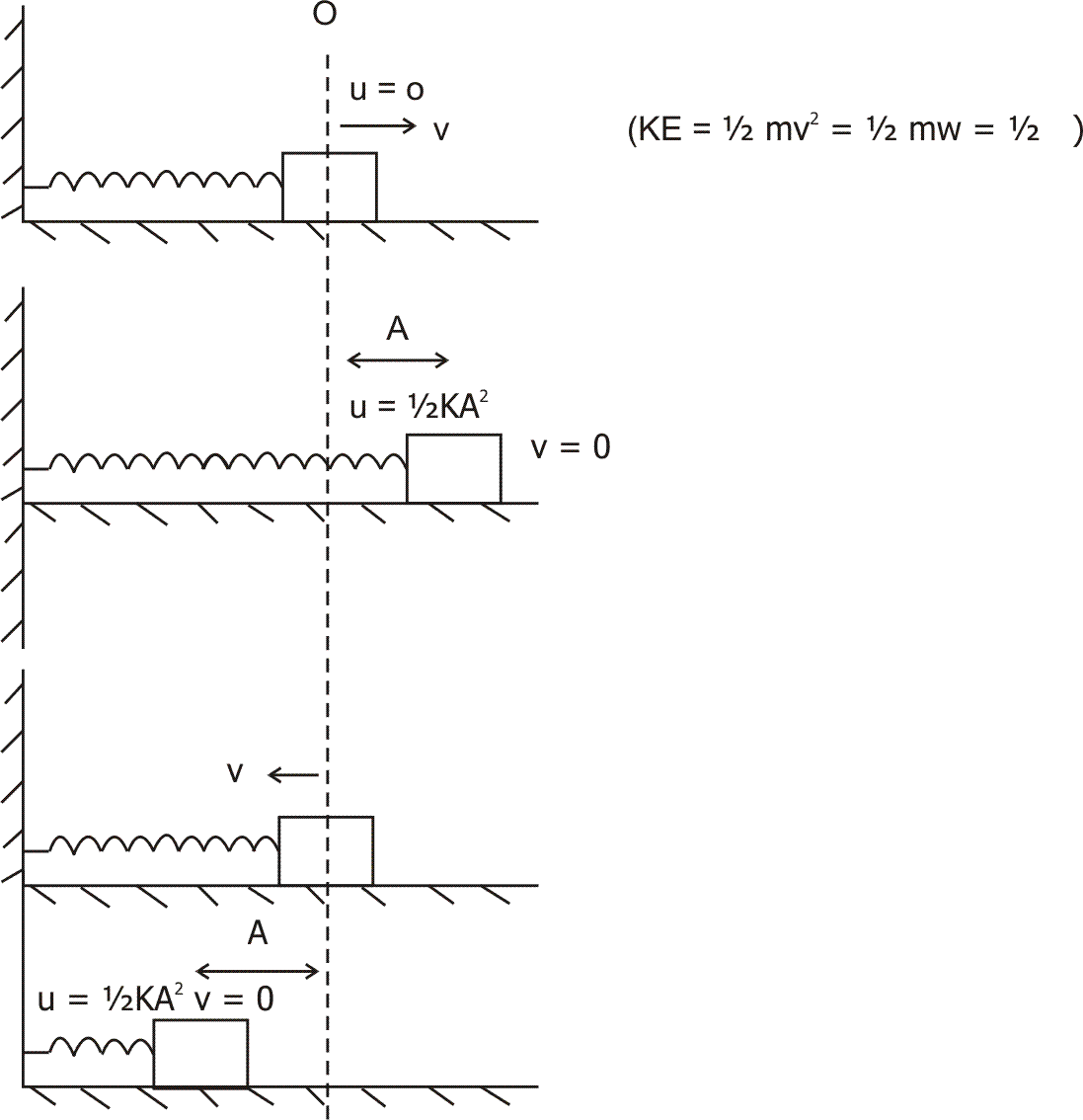
When at equilibrium position, it has velocity v and no potential energy as spring is relaxed. Hence the whole energy is in the form of KE. Now block moves towards right and its U increases. As Mechanical energy = Const. so its velocity decreases. Untill second situation where at the extreme position, the block stops, the K.E. goes to zero while PE increases to maximum value = Mechanical energy. Then the block moves left & process continues.


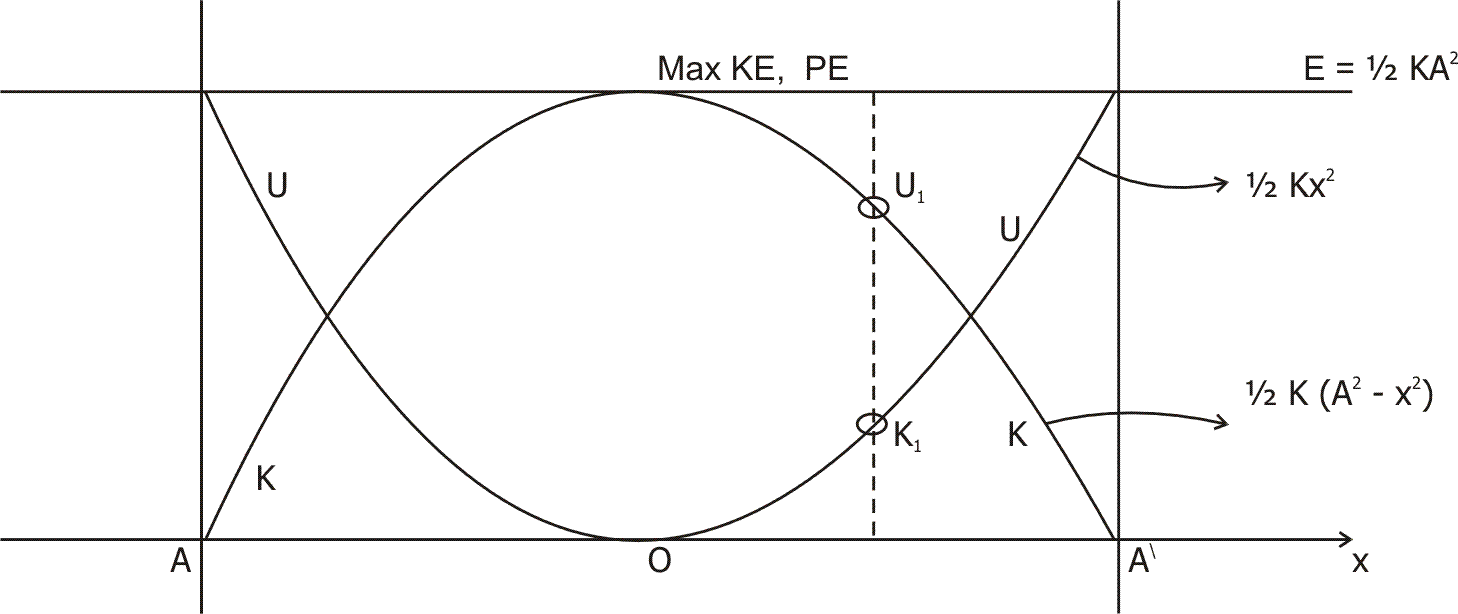
Explanation of above graph !
The Points A and 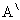are extreme position while O is the mean position. The U (Potential Energy) variation is shown. As expected U is minimum(= 0) at ‘O’ since sapring comes to natural state. The Maximum value of U occure at both extreme position where extension = maximum.
Similarly K is zero (minimum) at extreme position since at extreme positions, v = 0 and v = max when block croses the mean position, so K is maximum at O.
Note that at any instant, if 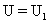then 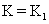= constant = .
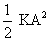* Algorithm for finding time period of a SHM :-
There are two methods - (I) Force/Tarqu`e method.
(II) Energy method.
(I) Force/Tarque mehod :-
Steps:(1) Find the mean position of system. Here net force/tarque is zero.
(2) Dispace the particle from its mean points by a small distance ‘x’.
(3) Now find the forces acting on particle.
(4) Write the equation as :

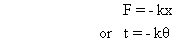
(5) Now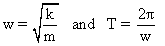
(II) Energy Method : (1) Find the mean position of system.
(2) Displace the particle from its mean position by small distance ‘x’.
(3) In SHM, mechanical energy remain constant, hence find the total mechanical energy of system in displaced position.
(4) Apply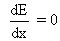
and use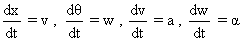
(5) Again using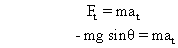


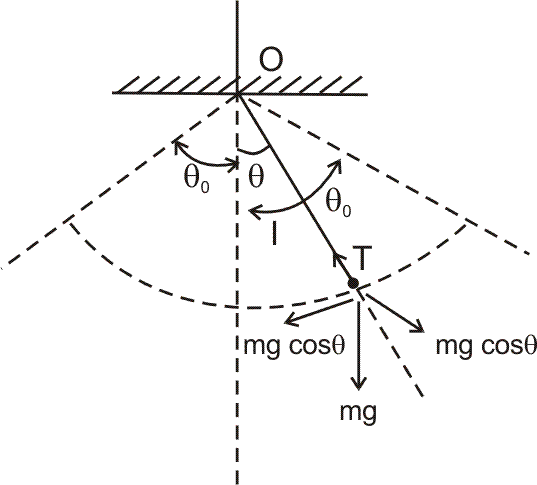
The tangental force acting will be 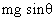while normal force will be T - .
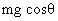Writing force equation in tangential direction.

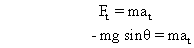
Now,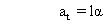

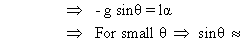
Hence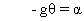
Compare with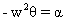

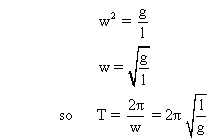
Dumb Question :- Why was the equation written in tengential direction ?
Solution :- The restoring force was in tange direction chence, the equation written in ’t' direction.
Dumb Question :- Why is 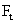negative ?
Solution :- 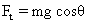is a restoring force, so its negative.
vertically using a spacing of constant ‘K’. If it is displaced slightly is time period?
Solution :-


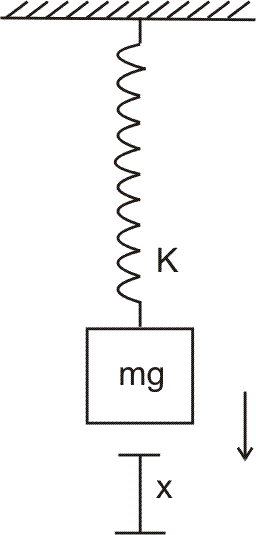
The equilibrium extension in spring is when

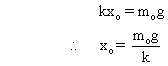
Now if further displaced ‘x’ then


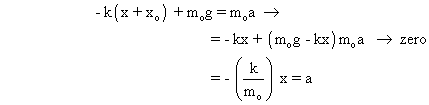
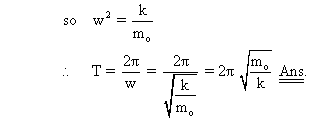
* Dumb Question :- Why is spring negative in (1) ?
Solution :-The block goes down as it is displaced, so the accelaration is downwards. The spring gives a restoring force app. to both ae in opposite directions.
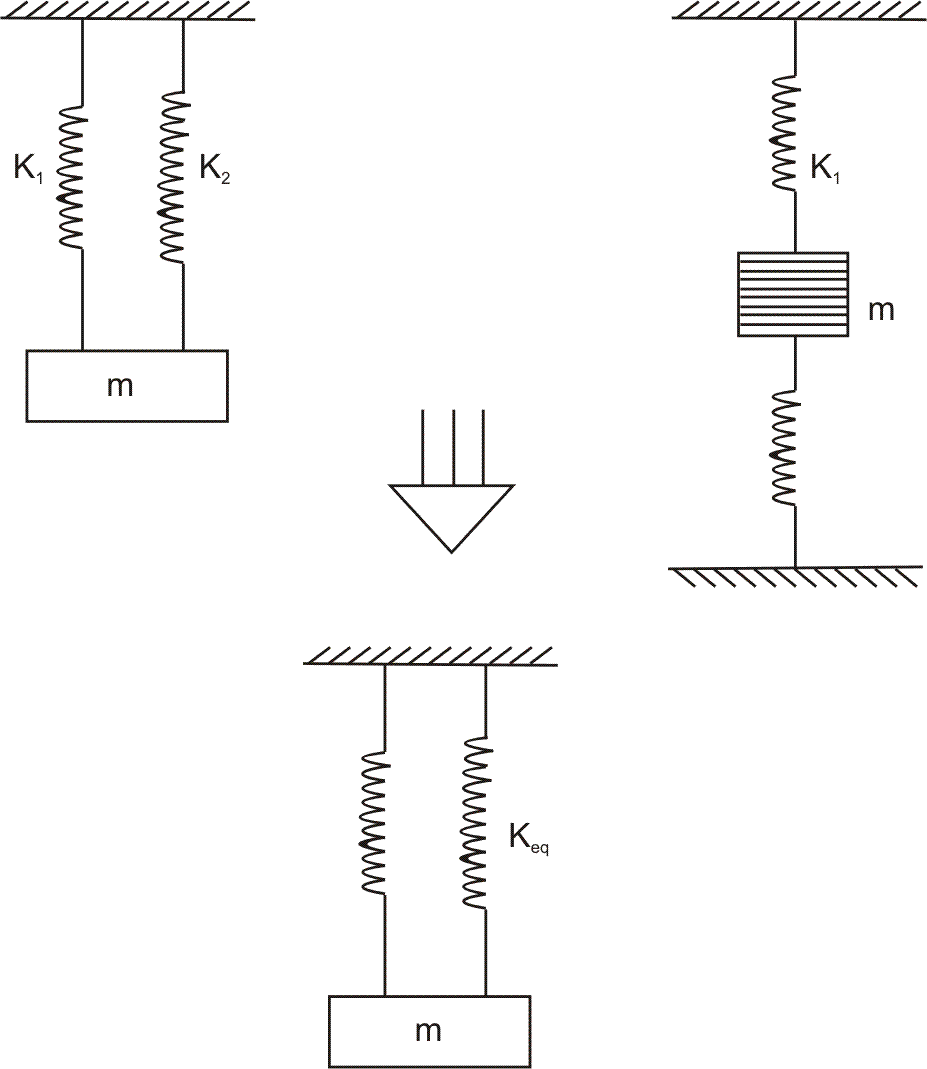
(1) Series Combination :


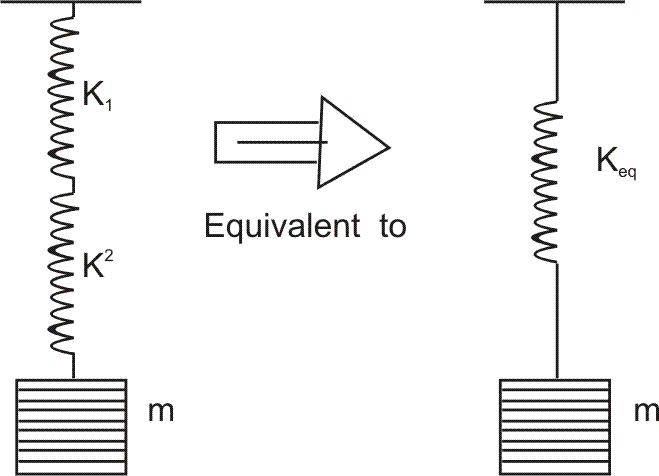
Here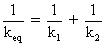
We can generalise this as :

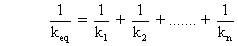
And hence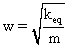
(2) Parellel Combination :