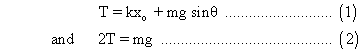SHM -6
Now, as the pulley is massless, this force 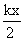 is equal to extra 2T or T =
is equal to extra 2T or T = 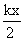 . this is also the restoring force of the mass.
. this is also the restoring force of the mass.
Hence
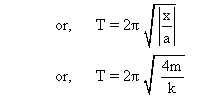
(c)
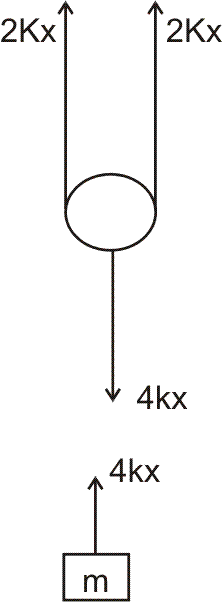
In this situation if the mass m moves down a distance x from its equilibrium position, the pulliey will also move by x and so the spring will stretch by 2x. therefore, the spring force will be 2kx. the restoring force on the block will be 4kx.
Hence,
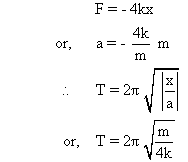
Question :-
spinning in opposite direction about their horizontal axes with equal angular velocity. The distance between the axes is 2l and the coefficient of friction between the plank and cylinder is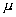 . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple Harmonic motion. Calculate also the time period of motion.
. If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple Harmonic motion. Calculate also the time period of motion.
Ans :-
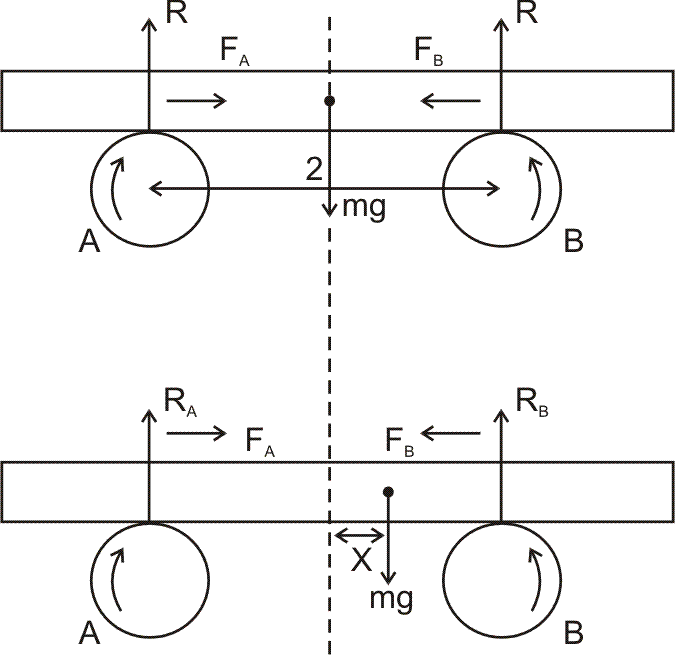
Now if the plank is displace by x to the right, the reactions not be equal. For vertical equilibrium of the plank -
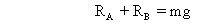 .................................. (1)
.................................. (1)
And for rotatinal of plank, taking moment about centre of mass we have,
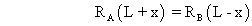 ................................... (2)
................................... (2)
Solving equations (1) and (2) we get,
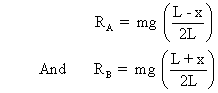
Now as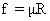 , so friction at B will be more than at A are will plank back. ie-
, so friction at B will be more than at A are will plank back. ie-
restoring force here -
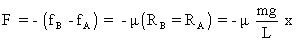
As the restoring force is linear, the motion will be simple harmonic motion with force constant -
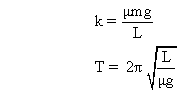
* Dumb Queation :- How to decide the direction of friction ?
Solution :-

The Roller A is moving clockwise. So friction always opposes the relative motion between the two bodies. Now friction tries to make the block move right so as to move along with roller A and hence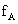 an block is towards right while
an block is towards right while 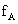 on roller A.
on roller A.
Similarly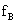 acts on block towards so as to make the block move towards left so that it moves with roller B which is moving anti clockwise.
acts on block towards so as to make the block move towards left so that it moves with roller B which is moving anti clockwise.
Question :-
goes over a pulling of mass and moment of inertia I, as shown in diagram. The string does not slip relative to the pulley.
Find the frequency of small oscillations.
Ans :-
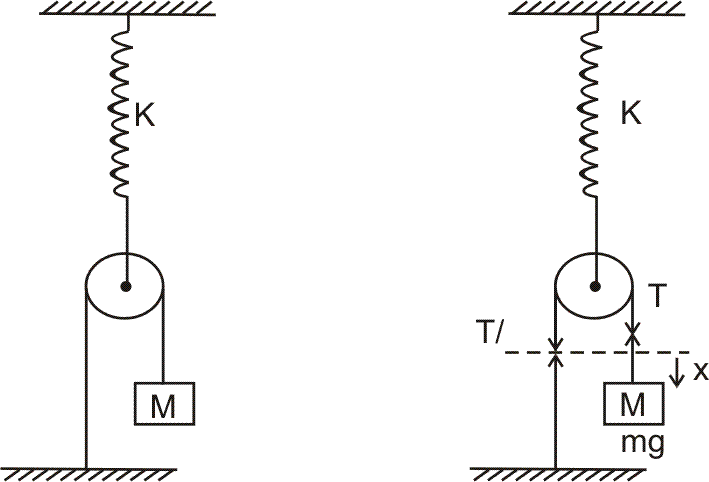
Suppose that the block is depressed by x. The pulley (owing to the constraint) is depressed by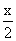 . Suppose that the tension in the string are T and
. Suppose that the tension in the string are T and 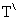 on both sides. We can write -
on both sides. We can write -
For block -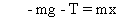 ...................................................... (1)
...................................................... (1)
For pulley -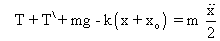 ............................. (2)
............................. (2)
The angular accelaration of the pulley,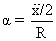 ................................ (3)
................................ (3)
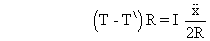 .................................................... (4)
.................................................... (4)
From (1), (2), (3) and (4) we get,
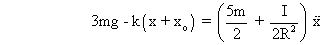 ........................ (5) The frequency of small oscillation,
........................ (5) The frequency of small oscillation,
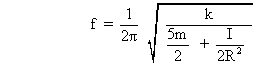
Question :-
lowest point O and is connected at the tangent point A by mean of a spring of spring constant K as shown in figure. Find the frequency of small oscillations. What is the condition for the system to perform small oscillations ?
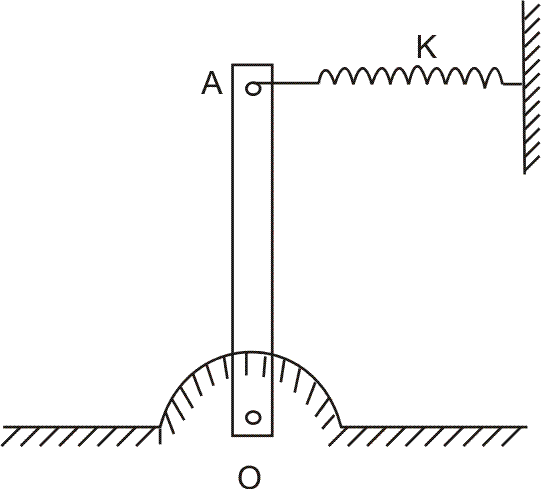
Ans :-
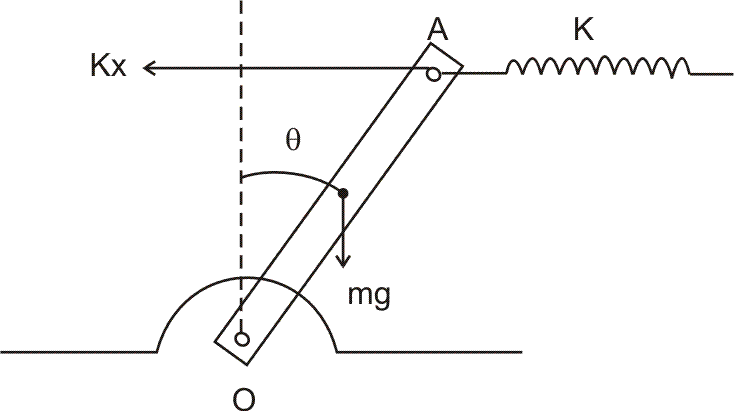
Suppose that the rod is displaced by a small angle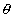 as shown in figure. The total mechanical energy of the system is given by:-
as shown in figure. The total mechanical energy of the system is given by:-
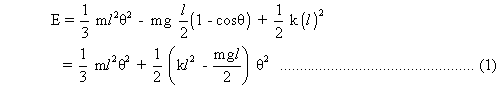
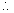 the angular frequency of small oscillation is,
the angular frequency of small oscillation is,
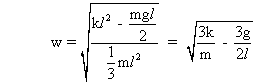 ........................................................(2)
........................................................(2)
the condition for the system to be oscillation is,

* Dumb Question :- How is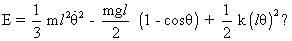
Solution :-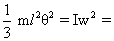 Rotational Kinetic energy of rod(gained)
Rotational Kinetic energy of rod(gained)
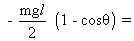 lass in potential energy of
lass in potential energy of
again in the potential energy of the spring.
There are all the energy terms.
Question :-
figure. Friction is absent everywhere and the threads and pulleys are massless. Given that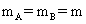 .
.
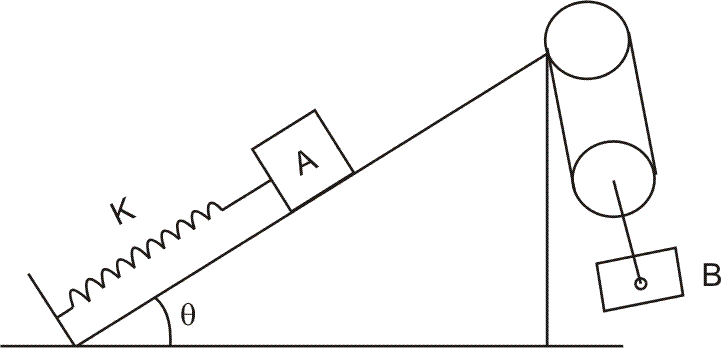
Ans :- Let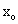 be the extension in the spring in equilibrium. then equilibrium of A and B give,
be the extension in the spring in equilibrium. then equilibrium of A and B give,
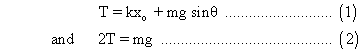
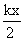 is equal to extra 2T or T =
is equal to extra 2T or T = 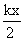 . this is also the restoring force of the mass.
. this is also the restoring force of the mass.Hence

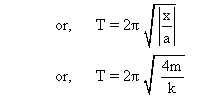
(c)

In this situation if the mass m moves down a distance x from its equilibrium position, the pulliey will also move by x and so the spring will stretch by 2x. therefore, the spring force will be 2kx. the restoring force on the block will be 4kx.
Hence,
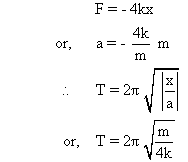
Question :-
spinning in opposite direction about their horizontal axes with equal angular velocity. The distance between the axes is 2l and the coefficient of friction between the plank and cylinder is
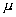 . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple Harmonic motion. Calculate also the time period of motion.
. If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple Harmonic motion. Calculate also the time period of motion.Ans :-

Now if the plank is displace by x to the right, the reactions not be equal. For vertical equilibrium of the plank -
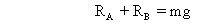 .................................. (1)
.................................. (1)And for rotatinal of plank, taking moment about centre of mass we have,
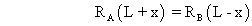 ................................... (2)
................................... (2)Solving equations (1) and (2) we get,
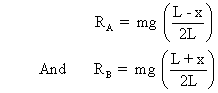
Now as
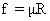 , so friction at B will be more than at A are will plank back. ie-
, so friction at B will be more than at A are will plank back. ie-restoring force here -
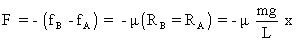
As the restoring force is linear, the motion will be simple harmonic motion with force constant -
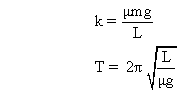
* Dumb Queation :- How to decide the direction of friction ?
Solution :-

The Roller A is moving clockwise. So friction always opposes the relative motion between the two bodies. Now friction tries to make the block move right so as to move along with roller A and hence
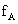 an block is towards right while
an block is towards right while 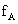 on roller A.
on roller A.Similarly
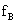 acts on block towards so as to make the block move towards left so that it moves with roller B which is moving anti clockwise.
acts on block towards so as to make the block move towards left so that it moves with roller B which is moving anti clockwise.Question :-
goes over a pulling of mass and moment of inertia I, as shown in diagram. The string does not slip relative to the pulley.
Find the frequency of small oscillations.
Ans :-

Suppose that the block is depressed by x. The pulley (owing to the constraint) is depressed by
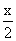 . Suppose that the tension in the string are T and
. Suppose that the tension in the string are T and 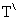 on both sides. We can write -
on both sides. We can write -For block -
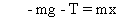 ...................................................... (1)
...................................................... (1)For pulley -
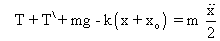 ............................. (2)
............................. (2)The angular accelaration of the pulley,
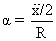 ................................ (3)
................................ (3)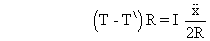 .................................................... (4)
.................................................... (4)From (1), (2), (3) and (4) we get,
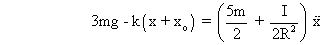 ........................ (5) The frequency of small oscillation,
........................ (5) The frequency of small oscillation,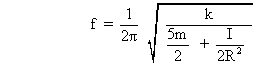
Question :-
lowest point O and is connected at the tangent point A by mean of a spring of spring constant K as shown in figure. Find the frequency of small oscillations. What is the condition for the system to perform small oscillations ?

Ans :-

Suppose that the rod is displaced by a small angle
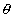 as shown in figure. The total mechanical energy of the system is given by:-
as shown in figure. The total mechanical energy of the system is given by:-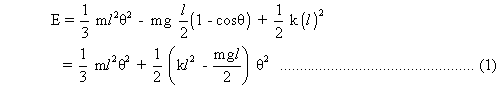
 the angular frequency of small oscillation is,
the angular frequency of small oscillation is,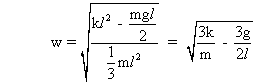 ........................................................(2)
........................................................(2)the condition for the system to be oscillation is,

* Dumb Question :- How is
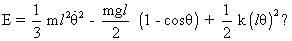
Solution :-
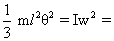 Rotational Kinetic energy of rod(gained)
Rotational Kinetic energy of rod(gained)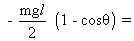 lass in potential energy of
lass in potential energy ofagain in the potential energy of the spring.
There are all the energy terms.
Question :-
figure. Friction is absent everywhere and the threads and pulleys are massless. Given that
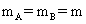 .
.
Ans :- Let
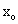 be the extension in the spring in equilibrium. then equilibrium of A and B give,
be the extension in the spring in equilibrium. then equilibrium of A and B give,