study material-physics-mechanics-shm superposition
SHM -7
Here, T is the tension in the string. Now, suppose A is further displaced by a distance x from its mean position and v be its speed at this moment. Then B lowers by 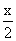 and speed B at this instant will be
and speed B at this instant will be 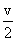 .
.
total energy of the system in this position will be,
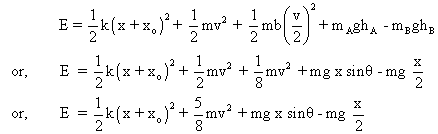
Since E is constant,
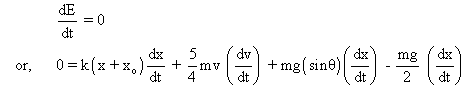
Substituting,
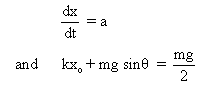 [from eqs. (1) and (2)]
[from eqs. (1) and (2)]
We get, 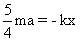
Since 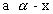

* Tip The energy method requires high accuracy for. writing the energy equation. A small mistake may lead to a wholly wrong answer.
Question :
Small angle about the vertical point passing through its middle point C The threads deviated in the process through an angle 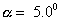 . Then the rod was released to start performing small oscillation energy.
. Then the rod was released to start performing small oscillation energy.
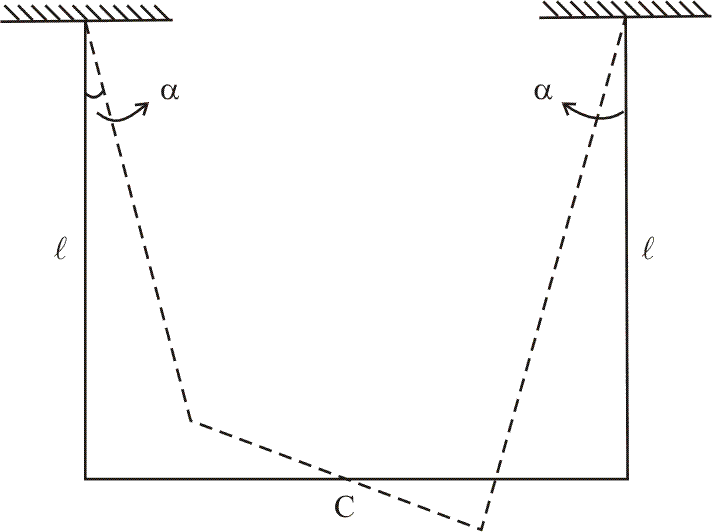
Find :-
(a) The oscillation period.
(b) The rod’s oscillation energy.
Ans :- In figure the rod is shown at a small angular displacement.
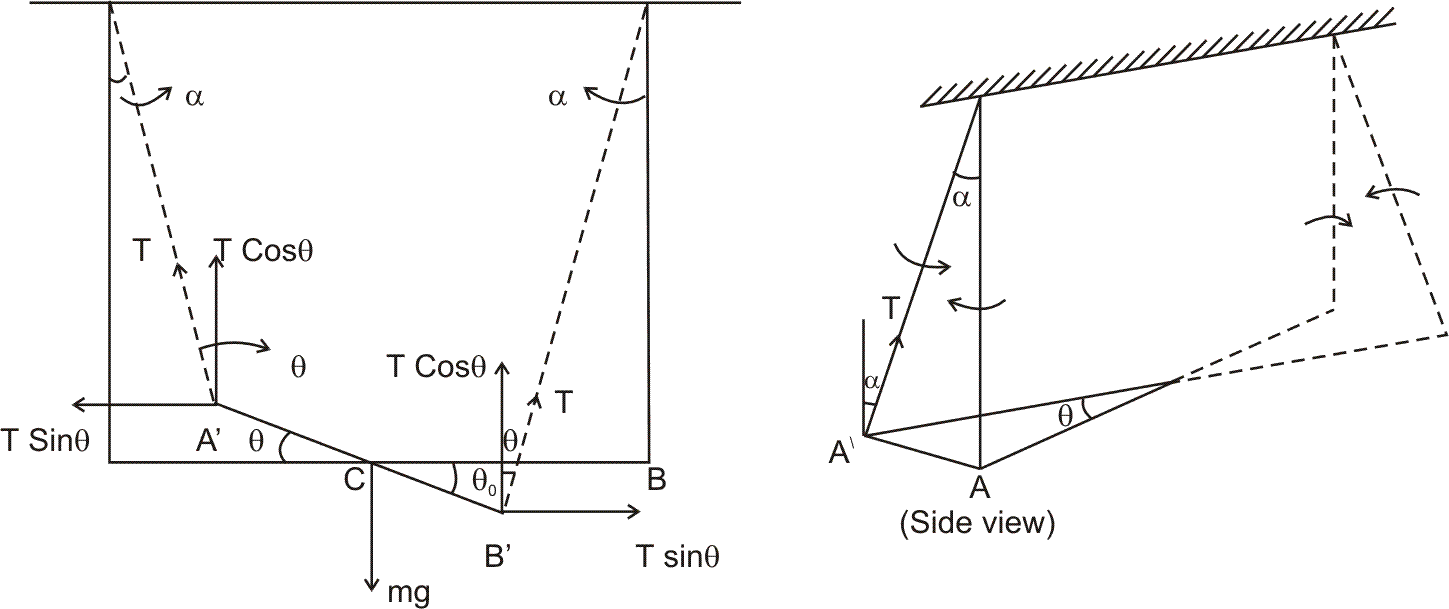
For trnslatory equilibrium of rod,
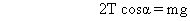
But 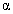 is very small.
is very small.
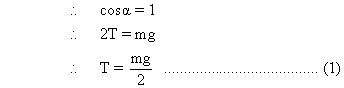
let 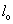 = length of rod. the torque about centre of rod in the direction of angular displacement is.
= length of rod. the torque about centre of rod in the direction of angular displacement is.
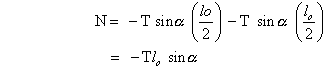
But 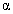 is very small.
is very small. 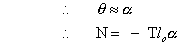
the moment of inertia of rod about centre of rod is -

From figure -
 and also
and also 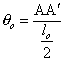
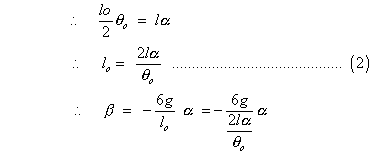

Hence inotion is angular S.H.M.
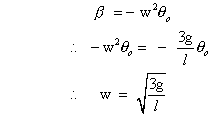
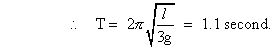
Question


 the oscillation energy is equal to maximum angular kinetic energy.
the oscillation energy is equal to maximum angular kinetic energy.
 the oscillation energy is -
the oscillation energy is -
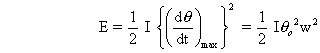
putting the value of I, w and 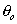 we get,
we get,
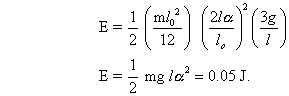
Question :-
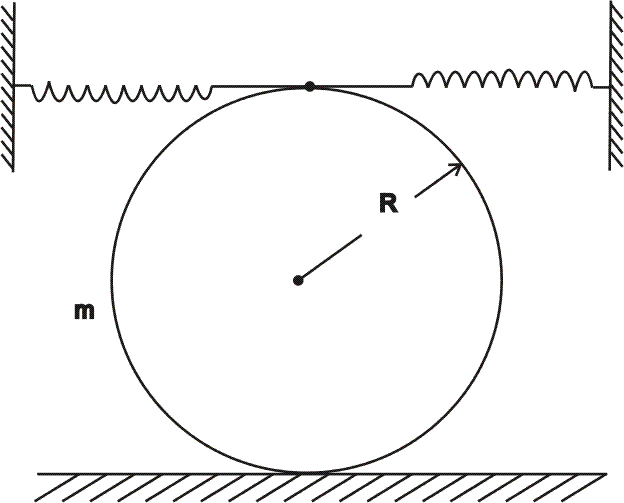
due to the action of two springs whose combined is equal to x. Find the period of these oscillations in the absence of sliding.
Ans :- When the centre of mass is displaced through a small distance x in rightward direction. Then the compression in rightward spring is 2x and elongation in leftward spring is 2x. the total mechanical energy of system at the displaced position is,
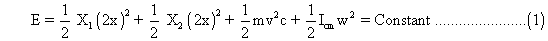
Also 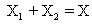
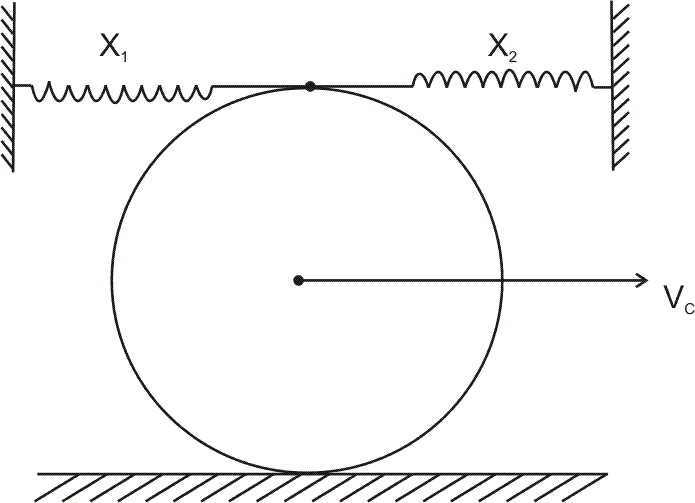
for pure ralling motion,

From equation (1),
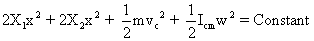
Differentiating both sides with repect to t,
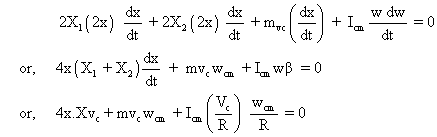
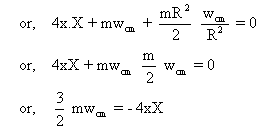
Hence motion is S.H.M. -
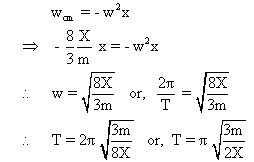
* Aplitude
* Time Period
* Frequency
* Angular Frequency
* Equation of SHM
* Phase
* Phase Constant
* Circular Representation of SHM
* Acceleration, Velocity in SHM
* Kinetic Energy in SHM
* Potential Energy in SHM
* Force Method for Time Period
* Energy Method for time Period
* Springs
* Combination of SHM’s.