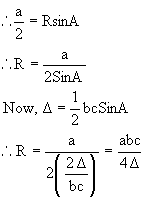solution-of-triangles-3

Area of Triangle ABC:

How?

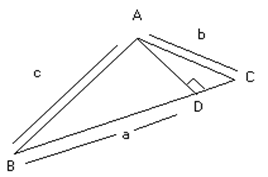
                                                            Fig (6)

Let there be a triangle ABC and draw a perpendicular AD on the side BC from A

So, now D = ½ AD.BC.

In triangle ABD

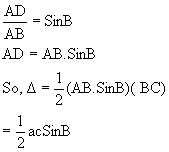
Why?

 

Solution: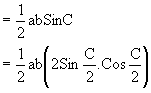

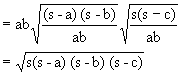
m-n theorem

 

If in a triangle ABC, point D divides BC in the ratio m: n and   ÐADC =Q then,

 

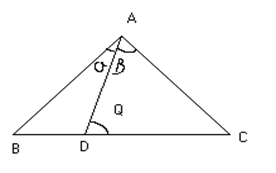
                                                                            Fig (7)

1)      (m+n) CotQ = mCotα-nCotβ

 

2)      (m+n) CotQ= nCotβ-mCotC

 

Illustration 5:

Find the value of y in

?

Ans:

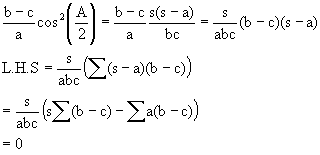
So, y = 0.

 

CIRCUMCIRCLE:

The Circle passing through points A, B, C of a triangle ABC, its radius is denoted by R.

 

How?

Bisect the 2 side BC and AC in D and E respectively and draw DO and EO perpendicular to BC and CA

                                      

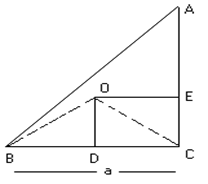
                                                           Fig (8)

So, O is center of circumcircle.

Now DBOD @DDOC     (By RHS congruency rule)    

So, ÐBOD = ÐDOC
                  = ½ ÐBOC
                  = ÐBAC
                  = ÐA
Now, in DBOD, BD = BO Sin (ÐBOD)