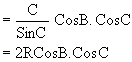solution-of-triangles-4
Illustration 6:
If in the DABC, O is circumcenter and R is the circumradius and R1, R2, R3, are circumradii of the triangle OBC, OCA, OAB respectively then prove that
![]()
Ans:
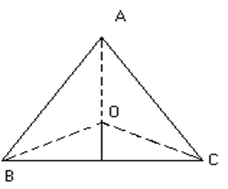
Fig (9)
Clearly in D OBC, ÐBOC = 2A,

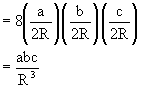
Incircle:
The Circle which touches all the sides of DABC internally its radius is denoted by r.
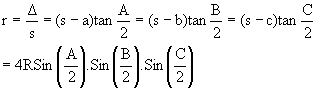
How?
Bisect the ÐB and ÐC by line BI and CI meeting in I
So now I is in center of the circle. Draw ID, IE and IF ^ to 3 sides.
So, ID = IE = IF = r
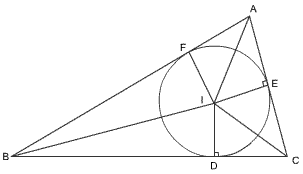
Fig (10)
Now we have
Area of DIBC = ½ ID.BC= ½ r.a
Area of DIAC = ½ IE.AC= ½ r.b
Area of DIAB = ½ IF.AB= ½ r.c
Area of DABC= area of DIBC + area of DIAC + area of DIAB.
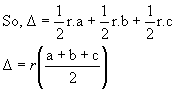
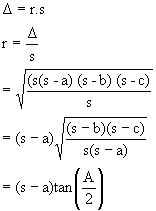
Now what about r = ![]()

Illustration7:
A, B, C are the angles of a triangle, prove that:
![]()
Ans:

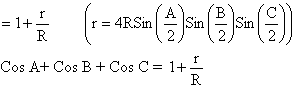
Excircles or Escribed circles:
The circle which touch BC and the two sides AB and AC produced is called escribed circle. Opposite the angle A and its radius is denoted by r1. Similarly radii of circle opposite the angle B and C are denoted by r2 and r3 respectively.
![]()
How?
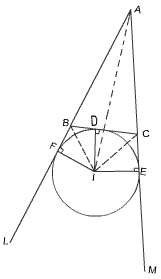
Fig (11)
Produce AB and AC to L and M. Bisect ÐCBL and ÐBCM by lines BI and CI and, let these lines meet in I.
Draw ID, IE, IF ^ to 3 sides respectively.
I is center of the escribed circle and so ID=IF=IE=r1.
Now area of DABC + area of DIBC = area of DIAB + area of DIAC
So, D+ ½ (ID) (BC) = ½ (IF) (AB) + ½ (IE) (AC)
Þ D + ½ r1a = ½ r1c + ½ r1b
So, D = ½ r1 (b+c-a)
= ½ r1 ((a+b+c)-2a)
= ½ r1 (2s-2a)
= r1 (s-a)

Now what about ![]()
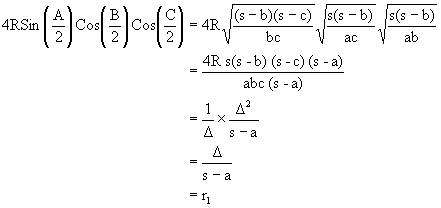
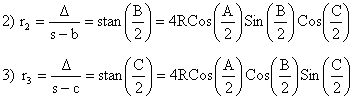
Illustration 8:
Show that ![]()
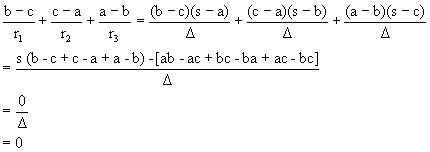
![]()
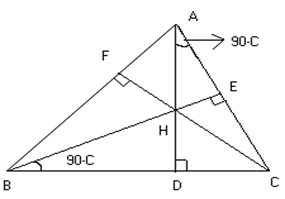
Orthocenter and Pedal D:
Let ABC be any triangle and let AD, BE and CF be the altitudes of DABC. Then the DDEF formed by joining point D, E and F the feet of ^ is called the pedal D of DABC.
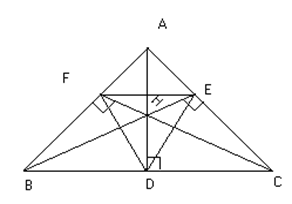
Fig (12)
Now
1) AH = 2RCosA, BH = 2RCosB, CH = 2CosC
How?
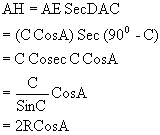
2) HD = 2R CosB CosC, HE = 2R CosA CosC, HF = 2R CosA CosB
Why?

Fig (14)
HD = BD tan ÐHBD
= BD tan (900 - c)
= AB CosB.CotC