solution-of-triangles-5

Illustration 9:

Prove that centroid, orthocenter and circumcenter of a D are collinear and centroid divides the line joining orthocenter and circumcenter in ratio 2:1.

Ans:

                                          

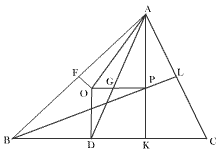
                                                             Fig (15)              

Let O and P be circumcenter and orthocenter respectively. Draw OD and PK ^ to BC.

Let AD and OP meet in G.

Now the DAGP and DDGO are equiangular which is clearly due to the fact that OD and PK are parallel lines.

Now OD = OB Cos ÐBOD

               = OB CosA

               = RCosA

Also AP = 2RCosA

So, by similar triangles,

So, point G is centroid of the D

Again by the same proposition

So, centroid divides line joining circumcenter to orthocenter in ratio 1:2.

Bisectors of theangles:

If AD is the angle bisector of ÐA then AD

                                                              

 

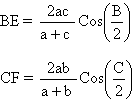
How?

                                     

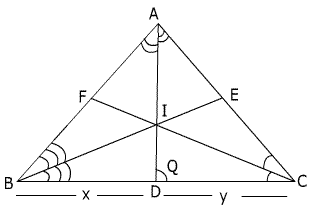
                                                                     Fig (16)

Now area of DABD + area of DADC = area of DABC

Þ ½ AB.AD Sin (A/2) + ½ AC.AD Sin (A/2) = ½ AB.AC SinA

Þ AD (AB Sin (A/2) + AC Sin (A/2)) = AB.AC.2Sin (A/2) Cos (A/2)

Þ AD (b+c) = 2bc Cos (A/2)

 

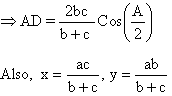
How?

Now in DABD

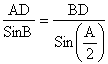
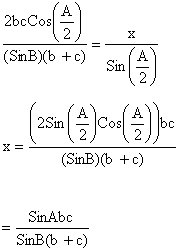
Now by using sine rule.

 

 

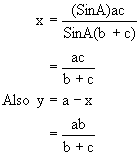
Medians:

 

If AD is a median then

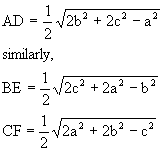
How?

                                

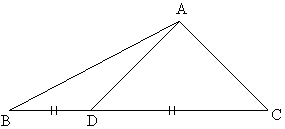
                                                         Fig (17)  

In DADC use cosine law

So AD² = AC²+DC²-2AC.DC.CosC

 

 

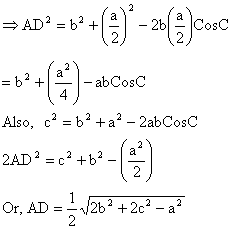
Illustration 10

In a DABC prove that  where AD is the median through A and

AD^AC

Ans:

                                 

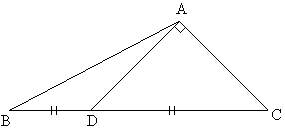
                                                                 Fig (18)         

 

 

In DADC

 AD² = DC²-AC²

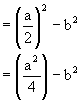
But

 

 

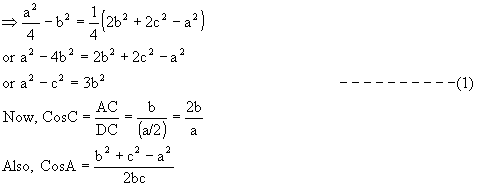
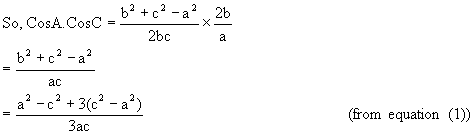
Solution of triangles 

When any 3 of the 6 elements (except all 3 angles) of a D given, the triangle is completely known. This process is called solution of triangle.

Case 1: When the sides a, b, c are given then how to find?

                                 

             Similarly B and C can be obtained.

 

Case 2: When two side’s b, c and included angle A are given then how to find?

                     

 So, B and C can be evaluated.

The third side is given by a

Case 3: When 2 sides’ b and c and angle B (opposite to side b) are given

1)      If angle B is acute.

a.      No triangle possible if b<cSinB

b.      One right angled D, right angled at C if b=cSinB

c.      two D’s are possible if cSinB<b<c

         

How?

           

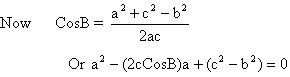
            So, for real values of a

           

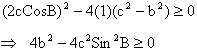
           \ If b<cSinB no triangle is possible.

                Now if b=cSinB

           Then   

           So, a right angle triangle with angle c= 90⁰ is possible

           Now,

           Is positive (B is acute)

           But if  is also be positive

           Then

           Or c²>b²

           Or c>b,

           So, if CSinB<b<c

           Then 2D’s are possible.

2)      If  ÐB is obtuse: only one D is possible if b>c

 

           How?

           CosB=

             Or

              a =

              Since B is obtuse CosB<0

              So, a cannot be  as it is less than zero.

               So, only possibility is a =  but this will be           

               Positive only if

               Or c²<b²

               Or c<b so, one D is possible if b>c.