solution-of-triangles-6

Q-3: If p, q are perpendiculars from the angular points A and B of the DABC drawn to any line

Through the vertex C then prove that

Solution:

Let ÐACE = a clearly from fig we get

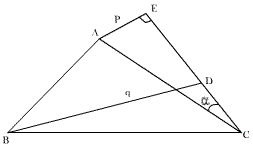
                                                Fig (21)        

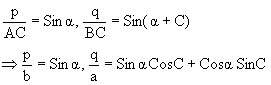
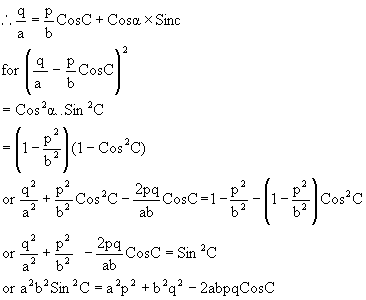
Q-4: Find the expression for area of cyclic quadrilateral.

Solution:  A quadrilateral is cyclic quadrilateral if its vertices lie on a circle.

Let ABCD be a cyclic quadrilateral such that AB=a, BC=b, CD=c and DA=d.

Then ÐB+ÐD = 180 and ÐA+ÐC = 180

Let 2s = a+b+c+d be the perimeter of the quadrilateral.

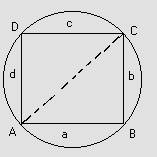
                                                                 Fig (22)

Now,    D = area of cyclic quadrilateral ABCD

                = area of DABC + area of DACD

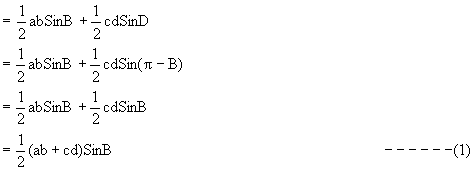
Using Cosine formula in a triangle ABC and ACD we have

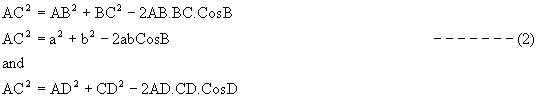
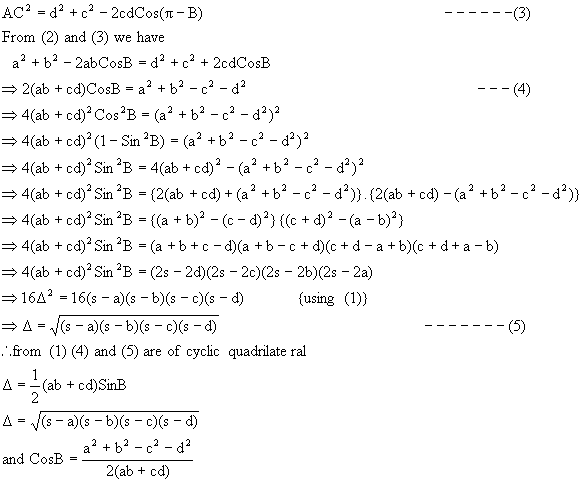
Q-5: Find the distance between the circumcenter and incenter.

Solution:

Let O be the circumcenter and I be the incenter of DABC. Let OF be perpendicular to AB and IE be perpendicular to AC and ÐOAF = 90-C.

\ÐOAI = ÐIAF-ÐOAF

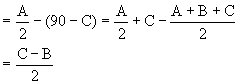
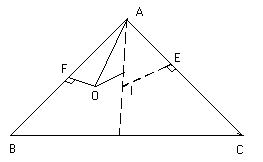
                                                               Fig (23)

Also,

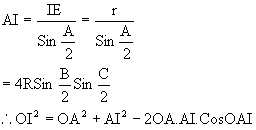
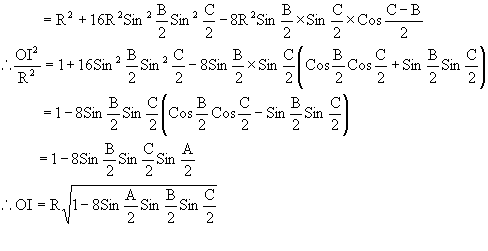
Q-6: Prove that  Where r = inradius, R=circum radius r₁, r₂, r₃ are exradii.

Solution:

L.H.S =  

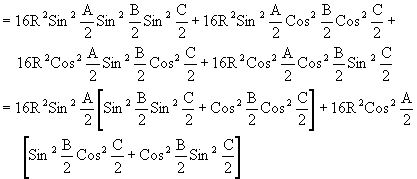
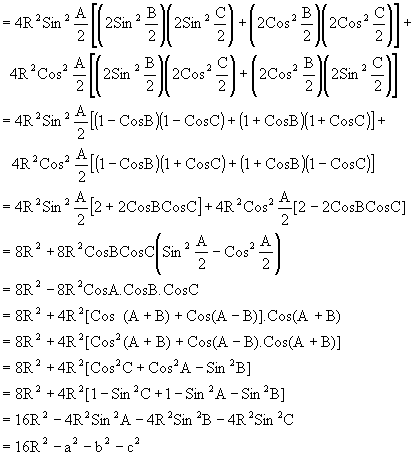
= R.H.S.