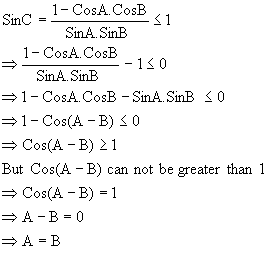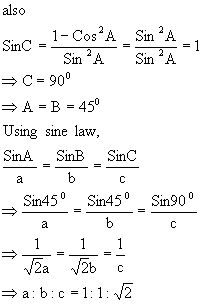solution-of-triangles-7

Q-7: Solve  in terms of K where K is perimeter of D ABC.

Solution:

Here,

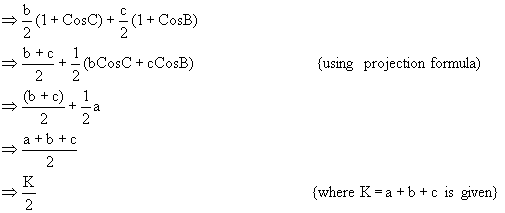
Q-8: Find the sides and angles of the pedal triangle.

Solution:

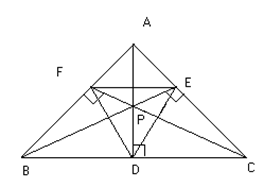
                                                Fig (19)

Since the angle PDC and PEC are right angles, the points P, E, C and D lie on a circle.

\ÐPDE = ÐPCE = 90-A

Similarly P, D, B and F lie on a circle and therefore

ÐPDF = ÐPBF = 90-A

Hence ÐFDE = 180-2A

Similarly ÐPEF = 180-2B

               ÐEFD = 180-2C

Also from triangle AEF we have

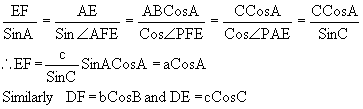
Q-9: Prove that in a DABC

Solution:

L.H.S =

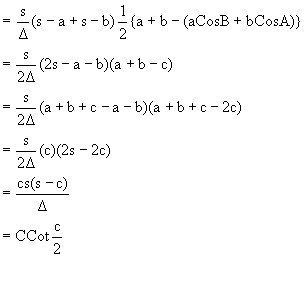
Q-10: Find the radii of the inscribed and the circumscribed circle of a regular polygon of n side

with each side and also find the area of the regular polygon.

Solution:

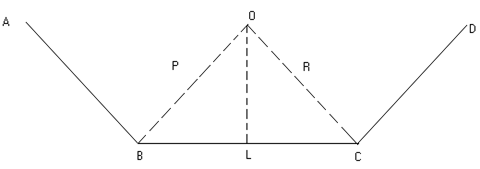
Fig (20)

Let AB, BC and CD be three successive sides of the polygon and O be the center of both

the incircle and the circumcircle of the

polygon.

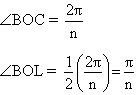
If a be a side of the polygon, we have a=BC=2BL=2RSinBOL =

Now the area of the regular polygon = n times the area of the DOBC

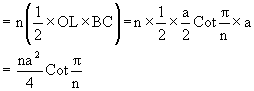
Q-11: If a₁b and A are given in a triangle and c₁, c₂ are the possible values of the third side,

prove that

Solution:

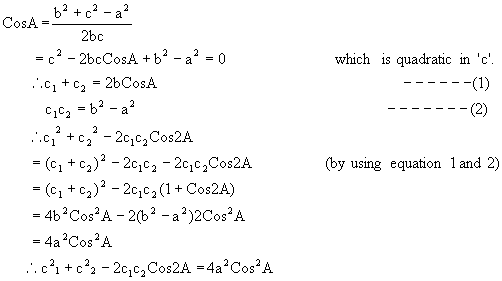
  Q-12: Prove that in a triangle the sum of exradii exceeds the inradius by twice the diameter of

the circumcircle.or prove that r₁+r₂+r₃ = r+4R.

Solution: Let the exradii be r_1, r_2, r₃ and inradius = r, circum radius = R.

Then we have to prove that r₁+r₂+r₃ = r+4R.

Now,

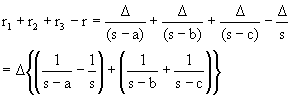
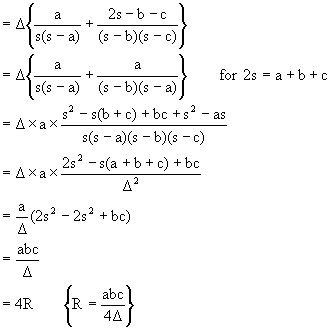
Medium

Q-1:

In a DABC the angles A, B, C are in A.P show that 

Solution:

Here, A, B, C are in A.P So B=A-a; C=A-2a

Also

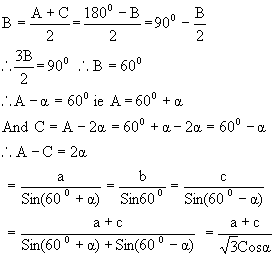
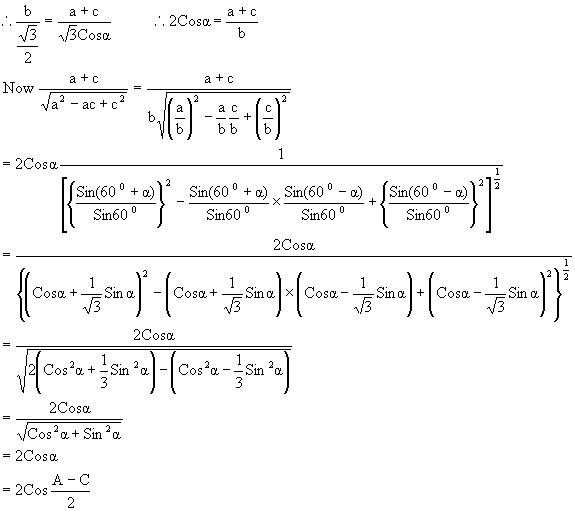
Q-2: If in a DABC, CosA.CosB+SinA.SinB.SinC = 1, Show that a: b: c = 1:1:Ö2

Solution: Given relation yields,